
(本小题满分10分)选修4~4:坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为?=6sin?.
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为?=6sin?.
(1)求圆C的直角坐标方程;
(2)若点P(1,2),设圆C与直线l交于点A,B.求∣PA∣+∣PB∣的最小值.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2016届甘肃省高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题10分)已知 =(cos
=(cos +sin
+sin ,-sin
,-sin ),
), =(cos
=(cos -sin
-sin ,2cos
,2cos ).
).
(1)设f(x)= ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈ ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年山东省高一10月月考数学试卷(解析版) 题型:填空题
定义:如果函数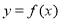 在定义域内给定区间
在定义域内给定区间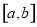 上存在
上存在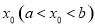 ,满足
,满足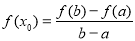 ,则称函数
,则称函数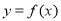 是
是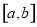 上的“平均值函数”,
上的“平均值函数”,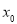 是它的一个均值点.如
是它的一个均值点.如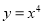 是
是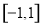 上的平均值函数,1是它的均值点.现有函数
上的平均值函数,1是它的均值点.现有函数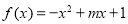 是区间
是区间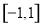 上的平均值函数,则实数
上的平均值函数,则实数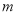 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省高一上学期一调数学试卷(解析版) 题型:填空题
设 是整数集的一个非空子集,对于
是整数集的一个非空子集,对于 ,如果
,如果 ,那么
,那么 是
是 的一个“孤立元”,给定
的一个“孤立元”,给定 ,则
,则 的所有子集中,只有一个“孤立元”的集合共有 个.
的所有子集中,只有一个“孤立元”的集合共有 个.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏省泰州市姜堰区高二上学期期中考试文科数学试卷(解析版) 题型:解答题
(本题满分16分)
设函数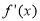 是奇函数
是奇函数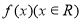 的导函数,
的导函数,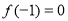 ,当
,当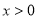 时,
时,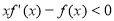 ,
,
(Ⅰ)判断函数 的奇偶性;
的奇偶性;
(Ⅱ)证明函数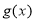 在
在 上为减函数;
上为减函数;
(Ⅲ)求不等式 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com