练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知随机变量ξ服从正态分布N（4，1），若P（3＜ξ≤5）=0.6826，则P（ξ＞5）=（　　）
    A．0.9544B．0.8413C．0.3174D．0.1587

    分析 根据随机变量ξ服从正态分布，知正态曲线的对称轴是x=4，且（3＜ξ≤5）=0.6826，欲求P（ξ＞5），只须依据正态分布对称性，即可求得答案．

    解答 解：由ξ服从正态分布N（4，1），得μ=4，σ=1．
    ∵P（3＜ξ≤5）=P（4-1＜ξ≤4+1）=0.6826，
    ∴$P（ξ＞5）=\frac{1}{2}×[1-P（3＜ξ≤5）]=0.1587$，
    故选：D．

    点评 本小题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．如果实数x，y满足约束条件$\left\{\begin{array}{l}x+2y-4≥0\\ x-y+2≥0\\ 2x+y-3≤0\end{array}\right.$，则（x+2）2+y2的最小值为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．椭圆$\frac{x^2}{{4{a^{\;}}}}+\frac{y^2}{{{a^2}+1}}=1（a＞0）$的焦点在x轴上，则它的离心率的最大值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{{\sqrt{2}}}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

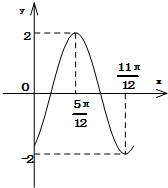
    17．函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（$\frac{π}{4}$）=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

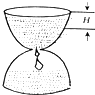    4．如图，现有一个计时沙漏，开始时盛满沙子，沙子从上部均匀下漏，经过5分钟漏完，H是该沙漏中沙面下降的高度，则H与下漏时间t（分）的函数关系用图象表示应该是（　　）
    A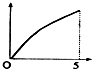．B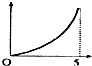．C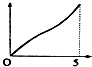．D．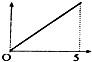

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数y=x3-3x+c的图象与x轴恰有两个公共点，求c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图所示，四边形ABCD是边长为2的菱形，且∠BAD=60°，四边形ABEF是正方形，平面ABCD⊥平面ABEF，点G，H分别为边CD，DA的中点，点M是线段BE上一动点．
    （1）求证：GH⊥DM；
    （2）求三棱锥D-MGH的体积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

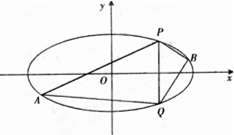    18．已知椭圆C的中心在原点，焦点在x轴上，离心率为$\frac{\sqrt{3}}{2}$，它的一个顶点恰好是抛物线x2=4$\sqrt{2}y$的焦点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）直线x=2与椭圆交于P，Q两点，P点位于第一象限，A，B是椭圆上位于直线x=2两侧的动点，满足直线PA与直线PB的倾斜角互补，证明直线AB的斜率为$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知数列{an}满足${a_1}=3，{a_{n+1}}={a_n}+2（n∈{N^*}）$，其前n项和为Sn，则$\frac{{4{S_n}+39}}{{4{a_n}}}$的最小值为（　　）
    A．$\frac{7}{2}$B．$\frac{99}{28}$C．$\frac{71}{20}$D．$\frac{51}{12}$

    查看答案和解析>>

    同步练习册答案