
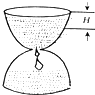
 如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )
如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )| A. | 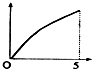 | B. | 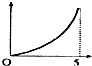 | C. | 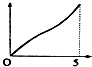 | D. | 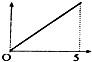 |
分析 利用特殊值法,圆柱液面上升速度是常量,表示圆锥漏斗中液体单位时间内落下的体积相同,当时间取$\frac{1}{2}$分钟时,液面下降高度与漏斗高度$\frac{1}{2}$的比较.
解答 解:利用特殊值法,圆柱液面上升速度是常量,表示圆锥漏斗中液体单位时间内落下的体积相同,当时间取1.5分钟时,液面下降高度与漏斗高度的$\frac{1}{2}$比较.
由于所给的圆锥形漏斗上口大于下口,当时间取$\frac{1}{2}$t时,漏斗中液面下落的高度不会达到漏斗高度的$\frac{1}{2}$,对比四个选项的图象可得结果.
故选:B
点评 本题考查函数图象,还可以正面分析得出结论:圆柱液面上升速度是常量,则V(这里的V是漏斗中剩下液体的体积)与t成正比(一次项),根据圆锥体积公式V=$\frac{1}{3}$πr2h,可以得出H=at2+bt中,a为正数,另外,t与r成反比,可以得出H=at2+bt中,b为正数.所以选择第二个答案.


科目:高中数学 来源: 题型:解答题
 已知椭圆方程$\frac{x^2}{2}+{y^2}=1$右焦点F、斜率为k的直线l交椭圆于P、Q两点.
已知椭圆方程$\frac{x^2}{2}+{y^2}=1$右焦点F、斜率为k的直线l交椭圆于P、Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.9544 | B. | 0.8413 | C. | 0.3174 | D. | 0.1587 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com