
分析 (1)因为f(x)为偶函数所以f(-x)=f(x)代入求得k的值即可;
(2)函数与直线没有交点即log9(9x+1)-$\frac{1}{2}$x=$\frac{1}{2}$x+a无解,即方程log9(9x+1)-x=a无解.令g(x)=log9(9x+1)-x,则函数y=g(x)的图象与直线y=b无交点.推出g(x)为减函数得到g(x)>0,所以让a≤0就无解.
(3)函数h(x)=f(x)-t(x)有且只有一个零点即函数f(x)与t(x)的图象有且只有一个公共点,即联立两个函数解析式得到方程,方程只有一个解即可.
解答 解:(1)因为y=f(x)为偶函数,
所以?x∈R,f(-x)=f(x),
即log9(9-x+1)-kx=log9(9x+1)+kx对于?x∈R恒成立.
即2kx=log9(9-x+1)-log9(9x+1)=log9( $\frac{{9}^{-x}+1}{{9}^{x}+1}$)=log9(9-x)=-x恒成立,
即(2k+1)x=0恒成立,
而x不恒为零,所以k=-$\frac{1}{2}$.
(2)由题意知方程log9(9x+1)-$\frac{1}{2}$x=$\frac{1}{2}$x+a即方程log9(9x+1)-x=a无解.
令g(x)=log9(9x+1)-x,则函数y=g(x)的图象与直线y=a无交点.
因为g(x)=log9( $\frac{{9}^{x}+1}{{9}^{x}}$)=log9(1+$\frac{1}{{9}^{x}}$),
任取x1、x2∈R,且x1<x2,则0<9x1<9x2,从而 $\frac{1}{{9}^{{x}_{1}}}$>$\frac{1}{{9}^{{x}_{2}}}$.
于是log9(1+$\frac{1}{{9}^{{x}_{1}}}$)>log9(1+$\frac{1}{{9}^{{x}_{2}}}$),即g(x1)>g(x2),
所以g(x)在(-∞,+∞)是单调减函数,
因为1+$\frac{1}{{9}^{x}}$>1,所以g(x)=log9(1+$\frac{1}{{9}^{x}}$)>0,
所以a的取值范围是(-∞,0).
(3)若函数h(x)=f(x)-t(x)有且只有一个零点,
则方程3x+$\frac{1}{{3}^{x}}$=m•3x-$\frac{4}{3}$m有且只有一个实数根.
令3x=t>0,则关于t的方程(m-1)t2-$\frac{4}{3}$mt-1=0(记为(*))有且只有一个正根.
若m=1,则t=-$\frac{3}{4}$,不合题意,舍去;
若m≠1,则方程(*)的两根异号或有两相等正根.
由△=0⇒m=$\frac{3}{4}$或-3;
但m=$\frac{3}{4}$⇒t=-$\frac{1}{2}$,不合题意,舍去;
而m=-3⇒t=$\frac{1}{2}$;
方程(*)的两根异号?(m-1)•(-1)<0,即-m+1<0,解得:m>1.
综上所述,实数m的取值范围{-3}∪(1,+∞).
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | A=B=C | B. | A?C | C. | A∩C=B | D. | B∪C⊆C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
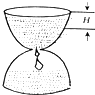 如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )
如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )| A. | 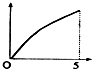 | B. | 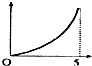 | C. | 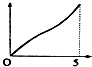 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四边形ABCD是边长为2的菱形,且∠BAD=60°,四边形ABEF是正方形,平面ABCD⊥平面ABEF,点G,H分别为边CD,DA的中点,点M是线段BE上一动点.
如图所示,四边形ABCD是边长为2的菱形,且∠BAD=60°,四边形ABEF是正方形,平面ABCD⊥平面ABEF,点G,H分别为边CD,DA的中点,点M是线段BE上一动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
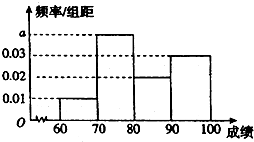 在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
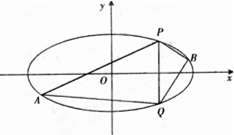 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}y$的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,它的一个顶点恰好是抛物线x2=4$\sqrt{2}y$的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com