
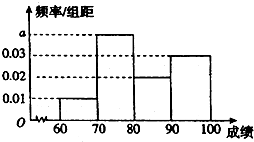
 在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
分析 (1)由频率分布直方图的性质先求出a,由此能估计这200名参赛选手的成绩平均数和中位数.
(2)根据题意知,成绩在(40,50],(50,60)内选手分别有1名和2名,随机变量X的取值为0,1,2,3.分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)因为10×(0.01+0.02+0.05+a)=1,
所以a=0.04.
平均数$\overline x=10×(65×0.01+75×0.04+85×0.02+95×0.03)=82$.
由图可知可视为两个矩形面积之和为0.5k,
则中位数为80.
(2)根据题意知,成绩在(40,50],(50,60)内选手分别有1名和2名,
随机变量X的取值为0,1,2,3.
$P(x=0)=\frac{1}{2}×{(\frac{1}{3})^2}=\frac{1}{18}$,
$P(x=1)=\frac{1}{2}×{(\frac{1}{3})^2}+\frac{1}{2}×C_2^1\frac{1}{3}×\frac{2}{3}=\frac{5}{18}$,
$P(x=2)=\frac{1}{2}×C_2^1\frac{1}{3}×\frac{2}{3}+\frac{1}{2}×{(\frac{2}{3})^2}=\frac{4}{9}$,
$P(x=3)=\frac{1}{2}×{(\frac{2}{3})^2}=\frac{2}{9}$.
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{18}$ | $\frac{5}{18}$ | $\frac{4}{9}$ | $\frac{2}{9}$ |
点评 本题考查频率分布直方图的性质及应用,考查离散型随机变量的分布列及数学期望的求法,是中档题,在历年高考中都是必考题型之一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
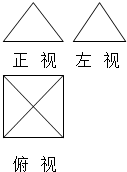 如图所示是一个几何体的三视图(单位:cm),主视图和左视图是底边长为4,腰长为$2\sqrt{2}$的等腰三角形,俯视图是边长为4的正方形,求几何体的表面积和体积.
如图所示是一个几何体的三视图(单位:cm),主视图和左视图是底边长为4,腰长为$2\sqrt{2}$的等腰三角形,俯视图是边长为4的正方形,求几何体的表面积和体积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com