
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 ①由独立性检验的特点说明正确;
②根据相关关系的相关指数R2的意义进行判断;
③已知随机变量ξ服从正态分布N(1,σ2),图象关于x=1对称,根据P(ξ≤4)=0.79,可得结论;
④设回归直线方程为y=2-2.5x,当变量x增加一个单位时,y平均减少2.5个单位.
解答 解:对于①,根据题意可得2×2列联表,求K2,再根据与临界值比较,检验这些中学生眼睛近视是否与性别有关,∴利用独立性检验的方法最有说服力,故①正确;
对于②,在相关关系中,若用${y_1}={c_1}{e^{{c_2}x}}$拟合时的相关指数为R12,用y2=bx+a拟合时的相关指数为R22,且R12>R22,则y1的拟合效果好,故②正确;
对于③,已知随机变量ξ服从正态分布N(1,σ2),图象关于x=1对称,根据P(ξ≤4)=0.79,可得P(ξ≤-2)=0.21,故③正确;
对于④,设回归直线方程为y=2-2.5x,当变量x增加一个单位时,y平均减少2.5个单位,故不正确.
∴正确命题的个数是3个,
故选:A.
点评 本题考查命题的真假判断与应用,考查了独立性检验、相关指数、正态分布、回归直线方程等知识点,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{4}$,1] | B. | [$\frac{3}{4}$,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
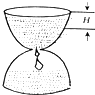 如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )
如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )| A. | 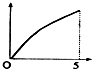 | B. | 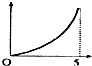 | C. | 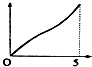 | D. | 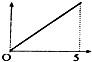 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四边形ABCD是边长为2的菱形,且∠BAD=60°,四边形ABEF是正方形,平面ABCD⊥平面ABEF,点G,H分别为边CD,DA的中点,点M是线段BE上一动点.
如图所示,四边形ABCD是边长为2的菱形,且∠BAD=60°,四边形ABEF是正方形,平面ABCD⊥平面ABEF,点G,H分别为边CD,DA的中点,点M是线段BE上一动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
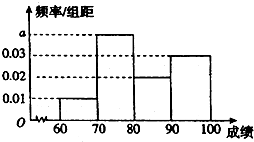 在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com