
分析 利用导数研究函数的单调性,可得极值与最值,又函数f(x)为R上的奇函数,且f(2)=0,可得图象:对x与-1的大小关系分类讨论即可得出.
解答 解:当x∈(1,+∞)时,f′(x)<0;当x∈(0,1)时,f′(x)>0,可知:当x=1时,函数f(x)取得极大值即为最大值,又函数f(x)为R上的奇函数,且f(2)=0,可得图象: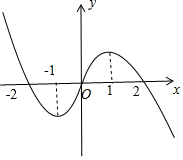
关于x的不等式(x+1)f(x)>0(x≠-1)等价于:
$\left\{\begin{array}{l}{x>-1}\\{f(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<-1}\\{f(x)<0}\end{array}\right.$,
解得:0<x<2,或-2<x<-1.
∴不等式(x+1)f(x)>0的解集为(-2,-1)∪(0,2).
故答案为:(-2,-1)∪(0,2).
点评 本题考查了利用导数研究函数的单调性极值最值与图象、函数的奇偶性、不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
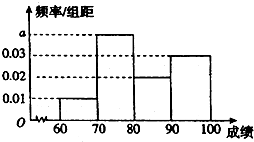 在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
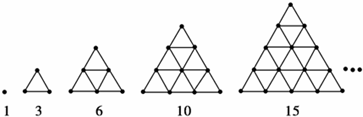
| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com