
分析 设等腰△ABC中A=B,由已知得sinA1=sinB1,cosA=sinA1,cosB=sinB1,cosC=sinC1,则A1=B1,结合同角三角函数关系进行化简求值即可.
解答 解:设A=B,由已知得sinA1=sinB1,cosA=sinA1,cosB=sinB1,cosC=sinC1,则A1=B1,
所以$A+{A_1}=\frac{π}{2}$,$B+{B_1}=\frac{π}{2}$,$C+{C_1}=\frac{π}{2}$(舍)或$A+{A_1}=\frac{π}{2}$,$B+{B_1}=\frac{π}{2}$,$C={C_1}-\frac{π}{2}$,
解得$C=\frac{π}{4}$.
故答案是:$\frac{π}{4}$.
点评 本题主要考查三角函数的化简求值,注意新定义运算法则,诱导公式的应用,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ②③ | C. | ④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
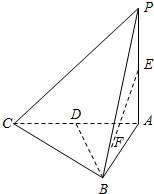 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
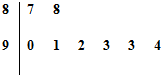 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91、5 | B. | 91、5.5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
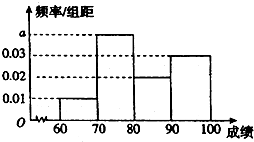 在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.
在某项娱乐活动的海选过程中,评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.| 参赛选手成绩所在区间 | (40,50] | (50,60) |
| 每名选手能够进入第二轮的概率 | $\frac{1}{2}$ | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2 | B. | ab | C. | $a\sqrt{{a^2}-{b^2}}$ | D. | $b\sqrt{{a^2}-{b^2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com