Question

1．以下四个命题中，正确的有（　　）
①两个底面平行且相似，其余各面都是梯形的多面体是棱台；
②有两个面平行，其余各面都是平行四边形的几何体叫做棱柱；
③在圆台上、下两底面的圆周上各取一点，则这两点的连线是圆台的母线；
④一个棱锥的各条棱长都相等，那么这个棱锥一定不是六棱锥．

• A． ①②④
• B． ②③
• C． ④
• D． ②④

Answer 1

分析 根据多面体的性质和几何体的定义来判断，采用举反例的方法来以及对概念的理解进行否定

解答 解：对于①，棱台还要求侧棱的延长线交于一点，故①错误，
对于②，有两个面平行其余各面都是平行四边形的几何体叫棱柱错误，即②错误，反例如图：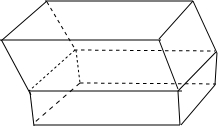

对于③，以直角梯形垂直于底边的腰所在直线为旋转轴，其余各边旋转而形成的曲面所围成的几何体叫做圆台．旋转轴叫做圆台的轴．直角梯形上、下底旋转所成的圆面称为圆台的上、下底面，另一腰旋转所成的曲面称为圆台的侧面，侧面上各个位置的直角梯形的腰称为圆台的母线，故③错误
对于④，以为正六棱锥的底面是个正六边形，正六边形共由6个等边三角形构成，设每个等边三角形的边长为 r，
正六棱锥的高为h，正六棱锥的侧棱长为 l，由正六棱锥的高 h、底面的半径 r、侧棱长l构成直角三角形得，
 h²+r²=l²，故侧棱长 l和底面正六边形的边长 r不可能相等，故④正确，
故选：C．

点评 本题考查的知识点是棱柱的几何特征，棱锥的几何特征，棱台的几何特征，熟练掌握相关定义是解答的关键，属于基础题．