
分析 (1)先设销售价为x元/瓶,则由题意知当月销售量,进而得出当月销售所得的利润;
(2)根据二次函数的性质求得f(x)取得最大值,即得答案.
解答 解:设销售价每瓶定为x元,利润为y元,则
(1)当月销售量为$\frac{4-x}{0.5}×40+400$=80(9-x)(瓶),
故当月销售所得的利润为y=80(9-x)(x-3)----(6分)
(2)y=80(9-x)(x-3)=-80(x-6)2+720(x≥3),
∴x=6时,y的最大值为720元-----(12分)
点评 本小题主要考查函数模型的选择与应用、二次函数的性质等,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{{e}^{2}}$ | B. | ln3-2 | C. | $\frac{3}{e}$-1 | D. | 3e-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
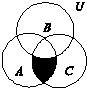 如图,已知U={1,2,3,4,5,6,7,8,9,10},集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为{2,8}.
如图,已知U={1,2,3,4,5,6,7,8,9,10},集合A={2,3,4,5,6,8},B={1,3,4,5,7},C={2,4,5,7,8,9},用列举法写出图中阴影部分表示的集合为{2,8}.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ②③ | C. | ④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
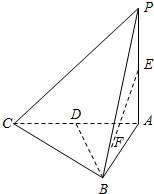 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com