
分析 由指数函数的值域判断①;举例说明②、③错误;由正弦定理及三角形中大边对大角判断④.
解答 解:对于①,∵ex>0,∴命题p:?x0∈R,${e^{x_0}}≤0$为假命题;
对于②,∵x=2时,x2-4x+4=0,∴命题q:?x∈R,x2-4x+4>0为假命题;
对于③,02=0×1,但0,0,1不是等比数列,∴“a,b,c成等比数列”的充分不必要条件是“b2=ac”为假命题;
对于④,在△ABC中,由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}$,可得由sinA>sinB?a>b?A>B,∴“sinA>sinB”是“A>B”的充要条件,故④为真命题.
故答案为:④.
点评 本题考查命题的真假判断与应用,考查了全程命题与特称命题的真假判断,考查充分必要条件的判定方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①②④ | B. | ②③ | C. | ④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
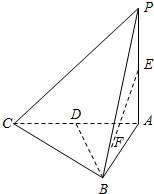 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2 | B. | ab | C. | $a\sqrt{{a^2}-{b^2}}$ | D. | $b\sqrt{{a^2}-{b^2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com