
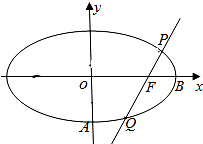
 已知椭圆方程$\frac{x^2}{2}+{y^2}=1$右焦点F、斜率为k的直线l交椭圆于P、Q两点.
已知椭圆方程$\frac{x^2}{2}+{y^2}=1$右焦点F、斜率为k的直线l交椭圆于P、Q两点.分析 (1)由题意方程求出b,c的值,代入菱形面积公式得答案;
(2)右焦点F(1,0),直线l的方程为y=x-1.设P(x1,y1),Q(x2,y2),由题设条件得y1=-1,${y}_{2}=\frac{1}{3}$.由此可求出△POQ的面积;
(3)假设在线段OF上存在点M(m,0)(0<m<1),使得以MP,MQ为邻边的平行四边形是菱形.因为直线与x轴不垂直,设直线l的方程为y=k(x-1)(k≠0).由题意知(1+2k2)x2-4k2x+2k2-2=0.由此可知0<m<$\frac{1}{2}$.
解答 解:(1)由椭圆方程$\frac{x^2}{2}+{y^2}=1$,得
a2=2,b2=1,则c2=a2-b2=1,
∴椭圆的两个焦点和短轴的两个端点构成的四边形的面积S=$\frac{1}{2}×2b×2c=\frac{1}{2}×2×2=2$;
(2)右焦点F(1,0),直线l的方程为y=x-1.
设P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}{y=x-1}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$,得3y2+2y-1=0,解得${y}_{1}=-1,{y}_{2}=\frac{1}{3}$.
∴${S}_{△POQ}=\frac{1}{2}$|OF|•|y1-y2|=$\frac{1}{2}$|y1-y2|=$\frac{2}{3}$;
(3)假设在线段OF上存在点M(m,0)(0<m<1),使得以MP,MQ为邻边的平行四边形是菱形.
∵直线与x轴不垂直,∴设直线l的方程为y=k(x-1)(k≠0).
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+{y}^{2}=2}\end{array}\right.$,可得(1+2k2)x2-4k2x+2k2-2=0.
∴${x}_{1}+{x}_{2}=\frac{4{k}^{2}}{1+{k}^{2}},{x}_{1}{x}_{2}=\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
$\overrightarrow{MP}=({x}_{1}-m,{y}_{1})$,$\overrightarrow{MQ}=({x}_{2}-m,{y}_{2})$,
$\overrightarrow{PQ}=({x}_{2}-{x}_{1},{y}_{2}-{y}_{1})$,(x2-x1≠0),
若以MP,MQ为邻边的平行四边形是菱形,则($\overrightarrow{MP}+\overrightarrow{MQ}$)⊥$\overrightarrow{PQ}$,
得,($\overrightarrow{MP}+\overrightarrow{MQ}$)•$\overrightarrow{PQ}$=0,
即(x1+x2-2m,y1+y2)(x2-x1,y2-y1)=0,
∴(x1+x2-2m)(x2-x1)+(y1+y2)(y2-y1)=0,则(x1+x2-2m)+k(y1+y2)=0,
∴($\frac{4{k}^{2}}{1+2{k}^{2}}$-2m)+k2($\frac{4{k}^{2}}{1+2{k}^{2}}$-2)=0,得2k2-(2+4k2)m=0,解得m=$\frac{{k}^{2}}{1+2{k}^{2}}$(k≠0).
∴0<m<$\frac{1}{2}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了平面向量在求解圆锥曲线问题中的应用,考查计算能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{4}$,1] | B. | [$\frac{3}{4}$,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B=C | B. | A?C | C. | A∩C=B | D. | B∪C⊆C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
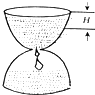 如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )
如图,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过5分钟漏完,H是该沙漏中沙面下降的高度,则H与下漏时间t(分)的函数关系用图象表示应该是( )| A. | 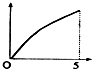 | B. | 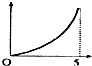 | C. | 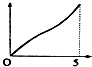 | D. | 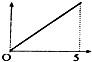 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com