
某巡逻艇在A处发现在北偏东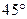 距A处8处有一走私船,正沿东偏南
距A处8处有一走私船,正沿东偏南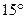 的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以
的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以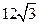 海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。
海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。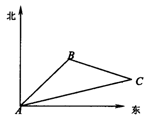
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
在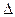 ABC中角A,B,C的对边分别为a,b,c,且满足(2a-c)cosB=bcosC
ABC中角A,B,C的对边分别为a,b,c,且满足(2a-c)cosB=bcosC
(1)求角B的大小;
(2设向量m= (sinA,cos2A),n=(k,1),且m n>1恒成立,求k的取值范围.
n>1恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题


11. (2009年高考辽宁卷)
如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰 角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01 km,
角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01 km,
≈1.414,≈2.449).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
、已知向量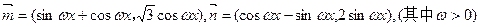 ,
,
函数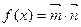 ,若
,若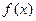 相邻两对称轴间的距离为
相邻两对称轴间的距离为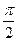 。
。
(1)求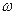 的值
的值 ,并求
,并求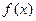 的最大值及相应x的集合;
的最大值及相应x的集合;
(2)在△ABC中,a,b,c分别是A,B,C所对的边,△AB C的面积
C的面积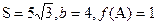 ,求边a的长。
,求边a的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com