
¡ŸÌâÄ¿¡¿Îª¹á³¹Âäʵµ³ÖÐÑëÈ«Ã朚ÉèС¿µÉç»áµÄÕœÂÔ²¿Êð£¬Ä³Æ¶À§µØÇøµÄ¹ãŽóµ³Ô±žÉ²¿ÉîÈëÅ©Žå»ýŒ«¿ªÕ¹¡°Ÿ«×Œ·öƶ¡±¹€×÷.Ÿ¹ý¶àÄêµÄŸ«ÐÄ°ï·ö£¬œØÖÁ2018Äêµ×£¬°ŽÕÕÅ©ŽåŒÒÍ¥ÈËŸùÄꎿÊÕÈë8000ÔªµÄС¿µ±ê׌£¬žÃµØÇøœöÊ£²¿·ÖŒÒÍ¥ÉÐΎʵÏÖС¿µ.2019Äê7Ô£¬Îª¹ÀŒÆžÃµØÄÜ·ñÔÚ2020ÄêÈ«ÃæʵÏÖС¿µ£¬Í³ŒÆÁ˞õص±Ê±×îƶÀ§µÄÒ»žöŒÒÍ¥2019Äê1ÖÁ6ÔµÄÈËŸùÔÂŽ¿ÊÕÈ룬×÷³öÉ¢µãÍŒÈçÏ£º

žùŸÝÏà¹ØÐÔ·ÖÎö£¬·¢ÏÖÆäŒÒÍ¥ÈËŸùÔÂŽ¿ÊÕÈë![]() ÓëʱŒäŽúÂë
ÓëʱŒäŽúÂë![]() Ö®ŒäŸßÓÐœÏÇ¿µÄÏßÐÔÏà¹Ø¹Øϵ£šŒÇ2019Äê1Ô¡¢2Ô¡¡·Ö±ðΪ
Ö®ŒäŸßÓÐœÏÇ¿µÄÏßÐÔÏà¹Ø¹Øϵ£šŒÇ2019Äê1Ô¡¢2Ô¡¡·Ö±ðΪ![]() £¬
£¬![]() £¬¡£¬ÒÀŽËÀàÍÆ£©£¬ÓɎ˹ÀŒÆžÃŒÒÍ¥2020ÄêÄÜʵÏÖС¿µÉú»î.µ«2020Äê1ÔÂÍ»ÈçÆäÀŽµÄйڷÎÑ×ÒßÇéÓ°ÏìÁ˱ŒÐ¡¿µµÄœøÕ¹£¬žÃŒÒÍ¥2020ÄêµÚÒ»ŒŸ¶ÈÿÔµÄÈËŸùÔÂŽ¿ÊÕÈëŸùÖ»ÓÐ2019Äê12ÔµÄÔ€¹ÀÖµµÄ
£¬¡£¬ÒÀŽËÀàÍÆ£©£¬ÓɎ˹ÀŒÆžÃŒÒÍ¥2020ÄêÄÜʵÏÖС¿µÉú»î.µ«2020Äê1ÔÂÍ»ÈçÆäÀŽµÄйڷÎÑ×ÒßÇéÓ°ÏìÁ˱ŒÐ¡¿µµÄœøÕ¹£¬žÃŒÒÍ¥2020ÄêµÚÒ»ŒŸ¶ÈÿÔµÄÈËŸùÔÂŽ¿ÊÕÈëŸùÖ»ÓÐ2019Äê12ÔµÄÔ€¹ÀÖµµÄ![]() .
.
£š1£©ÇóžÃŒÒÍ¥2020Äê3Ô·ݵÄÈËŸùÔÂŽ¿ÊÕÈË£»
£š2£©Èç¹ûÒԞÌÒÍ¥3Ô·ÝÈËŸùÔÂŽ¿ÊÕÈëΪ»ùÊý£¬ÒÔºóÿÔµÄÔö³€ÂÊΪ![]() £¬ÎªÊ¹žÃŒÒÍ¥2020ÄêÄÜʵÏÖС¿µÉú»î£¬
£¬ÎªÊ¹žÃŒÒÍ¥2020ÄêÄÜʵÏÖС¿µÉú»î£¬![]() ÖÁÉÙӊΪ¶àÉÙ£¿£šœá¹û±£ÁôÁœÎ»Ð¡Êý£©
ÖÁÉÙӊΪ¶àÉÙ£¿£šœá¹û±£ÁôÁœÎ»Ð¡Êý£©
²Î¿ŒÊýŸÝ£º![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() .
.
²Î¿Œ¹«Êœ£ºÏßÐԻع鷜³Ì![]() ÖУ¬
ÖУ¬ £¬
£¬![]() £»
£»
![]() £š
£š![]() £¬
£¬![]() £©.
£©.
¡ŸŽð°ž¡¿£š1£©500Ôª£»£š2£©0.07.
¡ŸœâÎö¡¿
£š1£©ÓÉÒÑÖªÇóµÃ![]() Óë
Óë![]() µÄÖµ£¬¿ÉµÃÏßÐԻع鷜³Ì£¬È¡
µÄÖµ£¬¿ÉµÃÏßÐԻع鷜³Ì£¬È¡![]() ÇóµÃ2019Äê12ÔžÌÒÍ¥ÈËŸùÔÂŽ¿ÊÕÈëÔ€¹ÀÖµ£¬œø¶ø¿ÉÇó³ö2020ÄêµÚÒ»ŒŸ¶ÈÿÔµÄÈËŸùÔÂŽ¿ÊÕÈ룬ŒŽ¿ÉµÃ³öŽð°ž£»
ÇóµÃ2019Äê12ÔžÌÒÍ¥ÈËŸùÔÂŽ¿ÊÕÈëÔ€¹ÀÖµ£¬œø¶ø¿ÉÇó³ö2020ÄêµÚÒ»ŒŸ¶ÈÿÔµÄÈËŸùÔÂŽ¿ÊÕÈ룬ŒŽ¿ÉµÃ³öŽð°ž£»
£š2£©ÉèŽÓ3Ô¿ªÊŒµœ12ÔµĎ¿ÊÕÈëÖ®ºÍΪ![]() £¬ÓÉÌâ¿ÉÖª
£¬ÓÉÌâ¿ÉÖª![]() £¬ÕûÀíµÃ
£¬ÕûÀíµÃ![]() £¬Çó³ö
£¬Çó³ö![]() µÄÈ¡Öµ·¶Î§£¬ŒŽ¿ÉµÃ³öŽð°ž.
µÄÈ¡Öµ·¶Î§£¬ŒŽ¿ÉµÃ³öŽð°ž.
£š1£©ÒÀÌâÒâµÃ£º![]() £¬
£¬![]() £¬
£¬
ËùÒÔ![]()
![]() £¬
£¬
![]() £¬
£¬
ËùÒÔ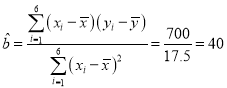 £¬
£¬
![]() £¬
£¬
ËùÒÔ![]() ¹ØÓÚ
¹ØÓÚ![]() µÄÏßÐԻع鷜³ÌΪ
µÄÏßÐԻع鷜³ÌΪ![]() .
.
Áî![]() ʱ£¬µÃ2019Äê12ÔžÌÒÍ¥ÈËŸùÔÂŽ¿ÊÕÈëÔ€¹ÀֵΪ
ʱ£¬µÃ2019Äê12ÔžÌÒÍ¥ÈËŸùÔÂŽ¿ÊÕÈëÔ€¹ÀֵΪ![]() Ôª£¬
Ôª£¬
ËùÒÔ£¬2020ÄêµÚÒ»ŒŸ¶ÈÿÔµÄÈËŸùÔÂŽ¿ÊÕÈëŸùΪ![]() Ôª£¬
Ôª£¬
ËùÒÔ£¬2020Äê3Ô·ݞÌÒÍ¥µÄÈËŸùÔÂŽ¿ÊÕÈëΪ500Ôª.
£š2£©ÒòΪÿÔµÄÔö³€ÂÊΪ![]() £¬ÉèŽÓ3Ô¿ªÊŒµœ12ÔµĎ¿ÊÕÈëÖ®ºÍΪ
£¬ÉèŽÓ3Ô¿ªÊŒµœ12ÔµĎ¿ÊÕÈëÖ®ºÍΪ![]() £¬Ôò
£¬Ôò
![]()
![]() £¬
£¬
ÒÀÌâÒ⣬Áî![]() £š*£©£¬
£š*£©£¬
µ±![]() ʱ£¬
ʱ£¬![]() £¬£š*£©³ÉÁ¢£»
£¬£š*£©³ÉÁ¢£»
µ±![]() ʱ£¬ÓÉ£š*£©µÃ
ʱ£¬ÓÉ£š*£©µÃ![]() £¬
£¬
ŒŽ![]() £¬
£¬
ËùÒÔ![]() £¬œâµÃ
£¬œâµÃ![]() »ò
»ò![]() £šÉáÈ¥£©£¬
£šÉáÈ¥£©£¬
×ÛÉϵãº![]() £¬
£¬
ËùÒÔ£¬ÎªÊ¹žÃŒÒÍ¥2020ÄêÄÜʵÏÖС¿µÉú»î£¬![]() ÖÁÉÙӊΪ
ÖÁÉÙӊΪ![]() .
.


 ÌìÌìÏòÉÏÒ»±ŸºÃŸíϵÁÐŽð°ž
ÌìÌìÏòÉÏÒ»±ŸºÃŸíϵÁÐŽð°ž СѧÉú10·ÖÖÓÓŠÓÃÌâϵÁÐŽð°ž
СѧÉú10·ÖÖÓÓŠÓÃÌâϵÁÐŽð°ž
| Äꌶ | žßÖÐ¿Î³Ì | Äꌶ | ³õÖÐ¿Î³Ì |
| žßÒ» | žßÒ»Ãâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍÆŒö£¡ |
| žß¶þ | žß¶þÃâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍÆŒö£¡ |
| žßÈý | žßÈýÃâ·Ñ¿Î³ÌÍÆŒö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍÆŒö£¡ |
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈôŽæÔÚ![]() £¬Ê¹µÃ
£¬Ê¹µÃ![]() ¶ÔÈÎÒâ
¶ÔÈÎÒâ![]() ºã³ÉÁ¢£¬Ôòº¯Êý
ºã³ÉÁ¢£¬Ôòº¯Êý![]() ÔÚ
ÔÚ![]() ÉÏÓÐÏœ磬ÆäÖÐ
ÉÏÓÐÏœ磬ÆäÖÐ![]() Ϊº¯Êý
Ϊº¯Êý![]() µÄÒ»žöÏœ磻ÈôŽæÔÚ
µÄÒ»žöÏœ磻ÈôŽæÔÚ![]() £¬Ê¹µÃ
£¬Ê¹µÃ![]() ¶ÔÈÎÒâ
¶ÔÈÎÒâ![]() ºã³ÉÁ¢£¬Ôòº¯Êý
ºã³ÉÁ¢£¬Ôòº¯Êý![]() ÔÚ
ÔÚ![]() ÉÏÓÐÉϜ磬ÆäÖÐ
ÉÏÓÐÉϜ磬ÆäÖÐ![]() Ϊº¯Êý
Ϊº¯Êý![]() µÄÒ»žöÉϜ磮Èç¹ûÒ»žöº¯ÊýŒÈÓÐÉÏœçÓÖÓÐÏœ磬ÄÇÃŽ³ÆžÃº¯ÊýÓМ磮
µÄÒ»žöÉϜ磮Èç¹ûÒ»žöº¯ÊýŒÈÓÐÉÏœçÓÖÓÐÏœ磬ÄÇÃŽ³ÆžÃº¯ÊýÓМ磮
ÏÂÊöËÄžöœáÂÛ£º¢Ù1²»ÊǺ¯Êý![]() µÄÒ»žöÏœ磻¢Úº¯Êý
µÄÒ»žöÏœ磻¢Úº¯Êý![]() ÓÐÏœ磬ÎÞÉϜ磻¢Ûº¯Êý
ÓÐÏœ磬ÎÞÉϜ磻¢Ûº¯Êý![]() ÓÐÉϜ磬ÎÞÏœ磻¢Üº¯Êý
ÓÐÉϜ磬ÎÞÏœ磻¢Üº¯Êý![]() ÓМ磮
ÓМ磮
ÆäÖÐËùÓÐÕýÈ·œáÂ۵ıàºÅÊÇ£š £©
A.¢Ù¢ÚB.¢Ú¢ÜC.¢Û¢ÜD.¢Ú
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬ËÄÀâ׶M£ABCDÖУ¬MB¡ÍÆœÃæABCD£¬ËıßÐÎABCDÊÇŸØÐΣ¬AB£œMB£¬E¡¢F·Ö±ðΪMA¡¢MCµÄÖе㣮
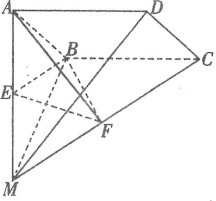
£š1£©ÇóÖ€£ºÆœÃæBEF¡ÍÆœÃæMAD£»
£š2£©Èô![]() £¬ÇóÈýÀâ׶E£ABFµÄÌå»ý£®
£¬ÇóÈýÀâ׶E£ABFµÄÌå»ý£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬Õý·œÌåABCD©A1B1C1D1µÄÀⳀΪ1£¬Ï߶ÎB1D1ÉÏÓÐÁœžö¶¯µãE¡¢F£¬ÇÒEF=![]() £®ÔòÏÂÁÐœáÂÛÖÐÕýÈ·µÄžöÊýΪ
£®ÔòÏÂÁÐœáÂÛÖÐÕýÈ·µÄžöÊýΪ
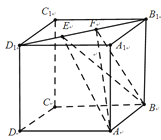
¢ÙAC¡ÍBE£»
¢ÚEF¡ÎÆœÃæABCD£»
¢ÛÈýÀâ׶A©BEFµÄÌå»ýΪ¶šÖµ£»
¢Ü![]() µÄÃæ»ýÓë
µÄÃæ»ýÓë![]() µÄÃæ»ýÏàµÈ£¬
µÄÃæ»ýÏàµÈ£¬
A.4B.3C.2D.1
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖª![]() ÊǶšÒåÔÚ
ÊǶšÒåÔÚ![]() ÉϵÄÅŒº¯Êý£¬ÆäÍŒÏó¹ØÓÚµã
ÉϵÄÅŒº¯Êý£¬ÆäÍŒÏó¹ØÓÚµã![]() ¶Ô³Æ.ÒÔϹØÓÚ
¶Ô³Æ.ÒÔϹØÓÚ![]() µÄœáÂÛ£º¢Ù
µÄœáÂÛ£º¢Ù![]() ÊÇÖÜÆÚº¯Êý£»¢Ú
ÊÇÖÜÆÚº¯Êý£»¢Ú![]() Âú×ã
Âú×ã![]() £»¢Û
£»¢Û![]() ÔÚ
ÔÚ![]() µ¥µ÷µÝŒõ£»¢Ü
µ¥µ÷µÝŒõ£»¢Ü![]() ÊÇÂú×ãÌõŒþµÄÒ»žöº¯Êý.ÆäÖÐÕýÈ·œáÂ۵ĞöÊýÊÇ( )
ÊÇÂú×ãÌõŒþµÄÒ»žöº¯Êý.ÆäÖÐÕýÈ·œáÂ۵ĞöÊýÊÇ( )
A.4B.3C.2D.1
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªÅ×ÎïÏß![]() µÄ׌ÏßÓëxÖáµÄœ»µãΪH£¬µãFΪÅ×ÎïÏߵĜ¹µã£¬µãPÔÚÅ×ÎïÏßÉÏÇÒ
µÄ׌ÏßÓëxÖáµÄœ»µãΪH£¬µãFΪÅ×ÎïÏߵĜ¹µã£¬µãPÔÚÅ×ÎïÏßÉÏÇÒ![]() £¬µ±k×îŽóʱ£¬µãPÇ¡ºÃÔÚÒÔH£¬FΪœ¹µãµÄË«ÇúÏßÉÏ£¬ÔòkµÄ×îŽóֵΪ_____£¬ŽËʱžÃË«ÇúÏßµÄÀëÐÄÂÊΪ_____£®
£¬µ±k×îŽóʱ£¬µãPÇ¡ºÃÔÚÒÔH£¬FΪœ¹µãµÄË«ÇúÏßÉÏ£¬ÔòkµÄ×îŽóֵΪ_____£¬ŽËʱžÃË«ÇúÏßµÄÀëÐÄÂÊΪ_____£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªÅ×ÎïÏß![]() µÄ׌ÏßÓëxÖáµÄœ»µãΪH£¬µãFΪÅ×ÎïÏߵĜ¹µã£¬µãPÔÚÅ×ÎïÏßÉÏÇÒ
µÄ׌ÏßÓëxÖáµÄœ»µãΪH£¬µãFΪÅ×ÎïÏߵĜ¹µã£¬µãPÔÚÅ×ÎïÏßÉÏÇÒ![]() £¬µ±k×îŽóʱ£¬µãPÇ¡ºÃÔÚÒÔH£¬FΪœ¹µãµÄË«ÇúÏßÉÏ£¬ÔòkµÄ×îŽóֵΪ_____£¬ŽËʱžÃË«ÇúÏßµÄÀëÐÄÂÊΪ_____£®
£¬µ±k×îŽóʱ£¬µãPÇ¡ºÃÔÚÒÔH£¬FΪœ¹µãµÄË«ÇúÏßÉÏ£¬ÔòkµÄ×îŽóֵΪ_____£¬ŽËʱžÃË«ÇúÏßµÄÀëÐÄÂÊΪ_____£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÒÑÖªÍÖÔ²![]() µÄ×󶥵ãΪ
µÄ×󶥵ãΪ![]() £¬ÓÒœ¹µãΪ
£¬ÓÒœ¹µãΪ![]() £¬µã
£¬µã![]() ÔÚÍÖÔ²
ÔÚÍÖÔ²![]() ÉÏ£®
ÉÏ£®
£š1£©ÇóÍÖÔ²![]() µÄ·œ³Ì£»
µÄ·œ³Ì£»
£š2£©ÈôÖ±Ïß![]() ÓëÍÖÔ²
ÓëÍÖÔ²![]() œ»ÓÚ
œ»ÓÚ![]() Áœµã£¬Ö±Ïß
Áœµã£¬Ö±Ïß![]() ·Ö±ðÓë
·Ö±ðÓë![]() Ö᜻ÓÚµã
Ö᜻ÓÚµã![]() £¬ÔÚ
£¬ÔÚ![]() ÖáÉÏ£¬ÊÇ·ñŽæÔÚµã
ÖáÉÏ£¬ÊÇ·ñŽæÔÚµã![]() £¬Ê¹µÃÎÞÂÛ·ÇÁãʵÊý
£¬Ê¹µÃÎÞÂÛ·ÇÁãʵÊý![]() ÔõÑù±ä»¯£¬×ÜÓÐ
ÔõÑù±ä»¯£¬×ÜÓÐ![]() ΪֱœÇ£¿ÈôŽæÔÚ£¬Çó³öµã
ΪֱœÇ£¿ÈôŽæÔÚ£¬Çó³öµã![]() µÄ×ø±ê£»Èô²»ŽæÔÚ£¬Çë˵Ã÷ÀíÓÉ£®
µÄ×ø±ê£»Èô²»ŽæÔÚ£¬Çë˵Ã÷ÀíÓÉ£®
²é¿ŽŽð°žºÍœâÎö>>
¿ÆÄ¿£ºžßÖÐÊýѧ ÀŽÔŽ£º ÌâÐÍ£º
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬ÔÚÈýÀâ׶![]() ÖУ¬µ×ÃæÊDZ߳€Îª4µÄÕýÈýœÇÐΣ¬
ÖУ¬µ×ÃæÊDZ߳€Îª4µÄÕýÈýœÇÐΣ¬![]() £¬
£¬![]() µ×Ãæ
µ×Ãæ![]() £¬µã
£¬µã![]() ·Ö±ðΪ
·Ö±ðΪ![]() £¬
£¬![]() µÄÖеã.
µÄÖеã.

£š1£©ÇóÖ€£ºÆœÃæ![]() ÆœÃæ
ÆœÃæ![]() £»
£»
£š2£©ÔÚÏ߶Î![]() ÉÏÊÇ·ñŽæÔÚµã
ÉÏÊÇ·ñŽæÔÚµã![]() £¬Ê¹µÃÖ±Ïß
£¬Ê¹µÃÖ±Ïß![]() ÓëÆœÃæ
ÓëÆœÃæ![]() Ëù³ÉµÄœÇµÄÕýÏÒֵΪ
Ëù³ÉµÄœÇµÄÕýÏÒֵΪ![]() £¿ÈôŽæÔÚ£¬È·¶šµã
£¿ÈôŽæÔÚ£¬È·¶šµã![]() µÄλÖã»Èô²»ŽæÔÚ£¬Çë˵Ã÷ÀíÓÉ.
µÄλÖã»Èô²»ŽæÔÚ£¬Çë˵Ã÷ÀíÓÉ.
²é¿ŽŽð°žºÍœâÎö>>
¹úŒÊѧУÓÅÑ¡ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·šºÍ²»ÁŒÐÅÏ¢ŸÙ±šÆœÌš | ÍøÉÏÓкŠÐÅÏ¢ŸÙ±š×šÇø | µçÐÅÕ©ÆŸÙ±š×šÇø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓкŠÐÅÏ¢ŸÙ±š×šÇø | ÉæÆóÇÖÈšŸÙ±š×šÇø
Î¥·šºÍ²»ÁŒÐÅÏ¢ŸÙ±šµç»°£º027-86699610 ŸÙ±šÓÊÏ䣺58377363@163.com