
【题目】若函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)证明:若![]() 存在零点,则
存在零点,则![]() 在区间
在区间![]() 上仅有一个零点.
上仅有一个零点.
【答案】(Ⅰ)![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;
;![]() 在
在![]() 处取得极小值
处取得极小值![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
试题分析:(Ⅰ)求单调区间和极值,先求定义域,再求导数![]()
![]() ,在
,在![]() 上,
上,![]() 的解为
的解为![]() ,探讨
,探讨![]() 在
在![]() 和
和![]() 上的正负,确定
上的正负,确定![]() 的单调性,极值;(Ⅱ)首先由零点存在,知最小值
的单调性,极值;(Ⅱ)首先由零点存在,知最小值![]() ,从而
,从而![]() ,因此
,因此![]() 在
在![]() 是单调递减,且
是单调递减,且![]() ,因此结论易证.
,因此结论易证.
试题解析:(Ⅰ)由![]() ,
,![]() 得
得
![]() .
.
由![]() 解得
解得![]() .
.![]() 与
与![]() 在区间
在区间![]() 上的情况如下:
上的情况如下:

所以,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;
;
![]() 在
在![]() 处取得极小值
处取得极小值![]() .
.
(Ⅱ)由(Ⅰ)知,![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
因为![]() 存在零点,所以
存在零点,所以![]() ,从而
,从而![]() .
.
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,且
上单调递减,且![]() ,
,
所以![]() 是
是![]() 在区间
在区间![]() 上的唯一零点.
上的唯一零点.
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,且
上单调递减,且![]() ,
,![]() ,
,
所以![]() 在区间
在区间![]() 上仅有一个零点.
上仅有一个零点.
综上可知,若![]() 存在零点,则
存在零点,则![]() 在区间
在区间![]() 上仅有一个零点.
上仅有一个零点.


科目:高中数学 来源: 题型:
【题目】侧棱垂直于底面的棱柱叫做直棱柱.
侧棱不垂直于底面的棱柱叫作斜棱柱.
底面是正多边形的直棱柱叫作正棱柱.
底面是平行四边形的四棱柱叫作平行六面体.
侧棱与底面垂直的平行六面体叫作直平行六面体.
底面是矩形的直平行六面体叫作长方体.
棱长都相等的长方体叫作正方体.
请根据上述定义,回答下面的问题(填“一定”、“不一定”“一定不”):
(1)直四棱柱________是长方体;
(2)正四棱柱________是正方体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
房屋面积x(m2) | 115 | 110 | 80 | 135 | 105 |
销售价格y(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线.
(参考公式![]() =
= ,
,![]() =
=![]()
![]() +
+![]() ,其中
,其中![]() =60 975,
=60 975,![]() =12 952)
=12 952)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,点
,点![]() 在椭圆上,
在椭圆上,![]() 、
、![]() 分别为椭圆的左右顶点,过点
分别为椭圆的左右顶点,过点![]() 作
作![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() ,
,![]() 为椭圆的右焦点.
为椭圆的右焦点.
(Ⅰ)求椭圆的方程及直线![]() 被椭圆截得的弦长
被椭圆截得的弦长![]() ;
;
(Ⅱ)求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 均为直线,
均为直线,![]() 为平面,下面关于直线与平面关系的命题:
为平面,下面关于直线与平面关系的命题:
①任意给定一条直线与一个平面![]() ,则平面
,则平面![]() 内必存在与
内必存在与![]() 垂直的直线;
垂直的直线;
②![]() 内必存在与
内必存在与![]() 相交的直线;
相交的直线;
③![]() ,必存在与
,必存在与![]() 都垂直的直线;
都垂直的直线;
其中正确命题的个数为( )
A.0个 B.1个
C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】社区服务是综合实践活动课程的重要内容,某市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
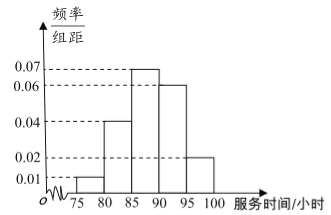
(1)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(2)从全市高中学生(人数很多)中任意选取3位学生,记![]() 为3位学生中参加社区服务时间不少于90小时的人数,试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数,试求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 是奇函数,函数
是奇函数,函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]() 上递减,根据单调性的定义求实数
上递减,根据单调性的定义求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数![]() 在区间
在区间![]() 上有且仅有两个不同的零点,求实数
上有且仅有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com