
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)求实数![]() 的取值范围,使
的取值范围,使![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)当![]() 时,
时,![]() ,可知函数的对称轴是
,可知函数的对称轴是![]() ,轴右边是单调递增区间,根据定义域求函数的单调递增区间;(2)若函数在
,轴右边是单调递增区间,根据定义域求函数的单调递增区间;(2)若函数在![]() 上是单调递增函数,那么区间不包含对称轴,即可写成
上是单调递增函数,那么区间不包含对称轴,即可写成![]() 的取值范围.
的取值范围.
试题解析:(1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,图象是抛物线,且开口向上,对称轴是x=1,所以,当x∈[-5,5]时,f(x)的单调递减区间是[-5,1],单调递增区间是[1,5];
(2)∵f(x)=x2+2ax+2,图象是抛物线,且开口向上,对称轴是x=-a;
当x∈[-5,5]时,若-a≤-5,即a≥5时, f(x)单调递增;若-a≥5,即a≤-5时,f(x)单调递减;
所以,f(x)在[-5,5]上是单调函数时,a的取值范围是(-∞,-5]∪[5,+∞)



科目:高中数学 来源: 题型:
【题目】空间四边形ABCD中,若AB=AD=AC=CB=CD=BD,则AC与BD所成角为 ( )
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 短轴的一个端点与其两个焦点构成面积为3的直角三角形.
短轴的一个端点与其两个焦点构成面积为3的直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,
, ![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过定点,如过,求出该定点;不过说明理由.
为直径的圆是否过定点,如过,求出该定点;不过说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:A商店以30元每条的价格销售,平均每日销售量为10条;B商店以25元每条的价格销售,平均每日销售量为20条。假定这种围巾的销售量t(条)是售价x(元)(![]() )的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
)的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润y(元)关于售价x(元)(![]() )的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
)的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润-总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为![]() ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.

(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
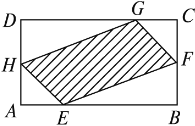
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积y最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为![]() 的圆
的圆![]() 与
与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点,另一圆
两点,另一圆![]() 与圆
与圆![]() 外切,且与
外切,且与![]() 轴及直线
轴及直线![]() 分别相切于
分别相切于![]() 、
、![]() 两点.
两点.
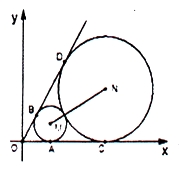
(1)求圆![]() 和圆
和圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 的平行线
的平行线![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得的弦的长度.
截得的弦的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com