
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
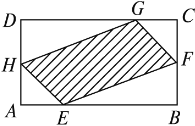
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积y最大?
【答案】(1) y=-2x2+(a+2)x(0<x≤2);(2)详见解析.
【解析】
试题分析:(1)可以用减法,整个矩形的面积-4个直角三角形的面积得到阴影面积,根据矩形边长求函数定义域,、;(2)函数配方后可得
![]() ,讨论对称轴
,讨论对称轴![]() 和定义域端点值2的关系,定义域若包含对称轴,那顶点最大,若定义域不包含对称轴,那离对称轴近函数值大,分情况得到函数的最大值.
和定义域端点值2的关系,定义域若包含对称轴,那顶点最大,若定义域不包含对称轴,那离对称轴近函数值大,分情况得到函数的最大值.
试题解析:(1)由题意可知,S△AEH=S△CGF=![]() ,S△DHG=S△BEF=
,S△DHG=S△BEF=![]() (a-x)(2-x),
(a-x)(2-x),
所以y=![]() -2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x.
-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x.
故函数解析式为y=-2x2+(a+2)x(0<x≤2).
(2)因为y=-2x2+(a+2)x (0<x≤2),
(0<x≤2),
当![]() ,即a<6时,则
,即a<6时,则![]() 时,y取最大值
时,y取最大值![]() ,
,
当![]() ,即a≥6时,y=-2x2+(a+2)x在x∈(0,2]上是增函数,
,即a≥6时,y=-2x2+(a+2)x在x∈(0,2]上是增函数,
则x=2时,y取最大值2a-4.
综上所述:当a<6时,AE=![]() 时,绿地面积取最大值
时,绿地面积取最大值![]() ;
;
当a≥6时,AE=2时,绿地面积取最大值2a-4.


科目:高中数学 来源: 题型:
【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
房屋面积x(m2) | 115 | 110 | 80 | 135 | 105 |
销售价格y(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线.
(参考公式![]() =
= ,
,![]() =
=![]()
![]() +
+![]() ,其中
,其中![]() =60 975,
=60 975,![]() =12 952)
=12 952)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 是奇函数,函数
是奇函数,函数![]() 的定义域为
的定义域为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]() 上递减,根据单调性的定义求实数
上递减,根据单调性的定义求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数![]() 在区间
在区间![]() 上有且仅有两个不同的零点,求实数
上有且仅有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级学生身体素质体能测试的成绩(百分制)分布在![]() 内,同时为了了解学生爱好数学的情况,从中随机抽取了
内,同时为了了解学生爱好数学的情况,从中随机抽取了![]() 名学生,这
名学生,这![]() 名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.
名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.

(1)求![]() 的值;
的值;
(2)用分层抽样的方法,从体能成绩在![]() 的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,求两名领队中恰有1人体能成绩在
的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,求两名领队中恰有1人体能成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 短轴的一个端点与其两个焦点构成面积为3的直角三角形.
短轴的一个端点与其两个焦点构成面积为3的直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过定点,如过,求出该定点;不过说明理由.
为直径的圆是否过定点,如过,求出该定点;不过说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com