练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】 一个几何体的三视图如图所示，已知正（主）视图是底边长为1的平行四边形，侧（左）视图是一个长为，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．

    （1）求该几何体的体积；

    （2）求该几何体的表面积．

    【答案】（1）；（2）．

    【解析】

    试题分析：（1）根据正视图是底面边长为的平行四边形，侧视图是个长为，宽为的矩形，得到该几何体是一个平行六面体，其底面是边长为的正方形，高为，即可求解体积；（2）由（1）看出的几何体，知道该平行六面体中，面，面，得到侧棱长，表示几何体的表面积，得到结果．

    试题解析：（1）由三视图可知，该几何体是一个平行六面体（如图），其底面是边长为1的正方形，高为，所以．

    （2）由三视图可知，该平行六面体中平面，平面，

    ∴，侧面，均为矩形，

    ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）判断函数的奇偶性，并加以证明；

    （2）用定义证明函数在区间上为增函数；

    （3）若函数在区间上的最大值与最小值之和不小于，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】社区服务是综合实践活动课程的重要内容，某市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据，按时间段，，，，（单位：小时）进行统计，其频率分布直方图如图所示.

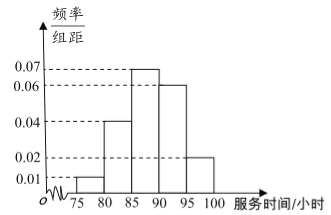
    （1）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；

    （2）从全市高中学生（人数很多）中任意选取3位学生，记为3位学生中参加社区服务时间不少于90小时的人数，试求随机变量的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列结论正确的是 （ ）

    A. 各个面都是三角形的几何体是三棱锥

    B. 以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥

    C. 棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥

    D. 圆锥的顶点与底面圆周上的任意一点的连线都是母线

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调递增区间；

    （2）求实数的取值范围，使在区间上是单调函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列几何体中是旋转体的是(　　)

    ①圆柱　②六棱锥　③正方体　④球体　⑤四面体

    A. ①和⑤ B. ①

    C. ③和④ D. ①和④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆短轴的一个端点与其两个焦点构成面积为3的直角三角形.

    （1）求椭圆的方程；

    （2）过圆上任意一点作圆的切线，与椭圆交于两点，以为直径的圆是否过定点，如过，求出该定点；不过说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线的方程是：，点．

    （1）若，直线过点且与曲线只有一个公共点，求直线的方程；

    （2）若曲线表示圆且被直线截得的弦长为，求实数的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知P＝{x|x2－8x－20≤0}，S＝{x|1－m≤x≤1＋m}.

    （1）是否存在实数m，使x∈P是x∈S的充要条件，若存在，求出m的范围；

    （2）是否存在实数m，使x∈P是x∈S的必要条件，若存在，求出m的范围.

    查看答案和解析>>

    同步练习册答案