[题目]设p:实数x满足x2﹣4ax+3a2＜0.其中a＞0, q:实数x满足＜0．(1)若a=1.且p∨q为真.求实数x的取值范围,(2)若p是q的必要不充分条件.求实数a的取值范围．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设p：实数x满足x2﹣4ax+3a2＜0，其中a＞0； q：实数x满足＜0．
（1）若a=1，且p∨q为真，求实数x的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．

【答案】
（1）解：由x2﹣4ax+3a2＜0，得（x﹣3a）（x﹣a）＜0，

又a＞0，所以a＜x＜3a，

当a=1时，1＜x＜3，即p为真时实数x的取值范围是1＜x＜3．

q为真时等价于（x﹣2）（x﹣3）＜0，得2＜x＜3，

即q为真时实数x的取值范围是2＜x＜3．

若p∨q为真，则实数x的取值范围是1＜x＜3

（2）解：p是q的必要不充分条件，等价于qp且p推不出q，

设A={x|a＜x＜3a}，B={x|2＜x＜3}，则BA；

则，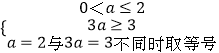

所以实数a的取值范围是1≤a≤2

【解析】（1）利用一元二次不等式的解法可化简命题p，q，若p∨q为真，则p，q至少有1个为真，即可得出；（2）根据p是q的必要不充分条件，即可得出．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在海岸线一侧有一休闲游乐场，游乐场的前一部分边界为曲线段，该曲线段是函数，的图像，图像的最高点为．边界的中间部分为长1千米的直线段，且．游乐场的后一部分边界是以为圆心的一段圆弧．

（1）求曲线段的函数表达式；
（2）曲线段上的入口距海岸线最近距离为1千米，现准备从入口修一条笔直的景观路到，求景观路长；
（3）如图，在扇形区域内建一个平行四边形休闲区，平行四边形的一边在海岸线上，一边在半径上，另外一个顶点P在圆弧上，且，求平行四边形休闲区面积的最大值及此时的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）在R上存在导函数f′（x），对于任意的实数x，都有f（x）=4x2﹣f（﹣x），当x∈（﹣∞，0）时，f′（x）+ ＜4x，若f（m+1）≤f（﹣m）+4m+2，则实数m的取值范围是（）
A.[﹣ ，+∞）
B.[﹣ ，+∞）
C.[﹣1，+∞）
D.[﹣2，+∞）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）是定义在R上的周期为4的奇函数，当0＜x＜2时，f（x）=4x ，则f（﹣ ）+f（2）= ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列命题中正确命题的个数是（） ①对于命题p：x∈R，使得x2+x+1＜0，则￢p：x∈R，均有x2+x+1＞0；
②命题“已知x，y∈R，若x+y≠3，则x≠2或y≠1”是真命题；
③回归直线的斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程为 =1.23x+0.08；
④m=3是直线（m+3）x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件．
A.1
B.3
C.2
D.4