
(12分)已知抛物线y2=8x上两个动点A、B及一个定点M(x0, y0),F是抛物线的焦点,且|AF|、|MF|、|BF|成等差数列,线段AB的垂直平分线与x轴交于一点N.
(1)求点N的坐标(用x0表示);
(2)过点N与MN垂直的直线交抛物线于P、Q两点,若|MN|=4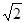 ,求△MPQ的面积.
,求△MPQ的面积.
(1)N(x0+4, 0);(2)64。
【解析】主要考查直线与抛物线的位置关系,等差数列知识以及转化与化归思想的运用。
(1)设A(x1, y1)、B(x2、y2),由|AF|、|MF|、|BF|成等差数列得x1+x2=2x0.
得线段AB垂直平分线方程: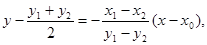
令y=0,得x=x0+4, 所以N(x0+4, 0).
(2)由M(x0, y0) , N(x0+4, 0), |MN|=4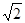 ,
得x0=2.
,
得x0=2.
由抛物线的对称性,可设M在第一象限,所以M(2, 4), N(6,0).
直线PQ: y=x-6, 由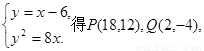 得△MPQ的面积是64.
得△MPQ的面积是64.
思路拓展:解答此题,等差数列知识在于确定量与量之间的关系;注意充分利用抛物线的几何性质—对称性。


 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||
B、x2-
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线y2=8x与椭圆
已知抛物线y2=8x与椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com