
【题目】已知函数f(x)= ![]() ,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
A.(0, ![]() )
)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.(0, ![]() ]
]
【答案】A
【解析】解:当x≤0时,由y= ![]() 得y2﹣9x2=1,(x≤0),此时对应的曲线为双曲线,双曲线的渐近线为y=﹣3x,此时渐近线的斜率k1=﹣3, 当x>0时,f(x)=1+xex﹣1 , 当过原点的直线和f(x)相切时,设切点为(a,1+aea﹣1),
得y2﹣9x2=1,(x≤0),此时对应的曲线为双曲线,双曲线的渐近线为y=﹣3x,此时渐近线的斜率k1=﹣3, 当x>0时,f(x)=1+xex﹣1 , 当过原点的直线和f(x)相切时,设切点为(a,1+aea﹣1),
函数的导数f′(x)=ex﹣1+xex﹣1=(x+1)ex﹣1 ,
则切线斜率k2=f′(a)=(a+1)ea﹣1 ,
则对应的切线方程为y﹣(1+aea﹣1)=(1+a)ea﹣1(x﹣a),
即y=(1+a)ea﹣1(x﹣a)+1+aea﹣1 ,
当x=0,y=0时,(1+a)ea﹣1(﹣a)+1+aea﹣1=0,
即a2ea﹣1+aea﹣1=1+aea﹣1 ,
即a2ea﹣1=1,得a=1,此时切线斜率k2=2,
则切线和y=﹣3x的夹角为θ,
则tanθ=| ![]() |=
|= ![]() ,则θ=
,则θ= ![]() ,
,
故∠AOB(O为坐标原点)的取值范围是(0, ![]() ),
),
故选:A.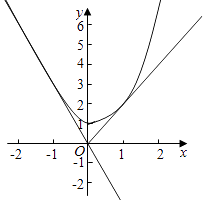


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,△BCD为正三角形,AD=AB=2, ![]() ,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.
,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°. 
(1)求证:平面PAC⊥平面PDB;
(2)求已知二面角A﹣PB﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个总体分为A,B两层,其个体数之比为5:1,用分层抽样方法从总体中抽取一个容量为12的样本,已知B层中甲、乙都被抽到的概率为 ![]() ,则总体中的个数为 .
,则总体中的个数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρ2﹣ρ2cos2θ=12.若曲线C的左焦点F在直线l上,且直线l与曲线C交于A,B两点.
(1)求m的值并写出曲线C的直角坐标方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣n.
(Ⅰ)证明数列{an+1}是等比数列,求数列{an}的通项公式;
(Ⅱ)记bn= ![]() +
+ ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某工厂![]() 和
和![]() 两车间工人掌握某技术情况,现从这两车间工人中分别抽查
两车间工人掌握某技术情况,现从这两车间工人中分别抽查![]() 名和
名和![]() 名工人,经测试,将这
名工人,经测试,将这![]() 名工人的测试成绩编成的茎叶图。若成绩在
名工人的测试成绩编成的茎叶图。若成绩在![]() 以上(包括
以上(包括![]() )定义为“良好”,成绩在
)定义为“良好”,成绩在![]() 以下定义为“合格”。已知
以下定义为“合格”。已知![]() 车间工人的成绩的平均数为
车间工人的成绩的平均数为![]() ,
,![]() 车间工人的成绩的中位数为
车间工人的成绩的中位数为![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 车间工人的成绩的方差;
车间工人的成绩的方差;
(3)在这![]() 名工人中,用分层抽样的方法从 “良好”和“及格”中抽取
名工人中,用分层抽样的方法从 “良好”和“及格”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,求至少有一人为“良好”的概率。
人,求至少有一人为“良好”的概率。
(参考公式:方差![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com