
某车间加工零件的数量 与加工时间
与加工时间 的统计数据如表:
的统计数据如表:
零件数 (个) (个) | 10 | 20 | 30 |
加工时间 (分钟) (分钟) | 21 | 30 | 39 |
 中的
中的 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( ) 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
一个总体分为A,B两层,其个体数之比为5:3,用分层抽样方法从总体中抽取一个容量为120的样本.则A层中应该抽取的个数为( )
| A.30 | B.45 | C.50 | D.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
10名工人某天生产同一种零件,生产的件数是15,17,14,10,15,17,17,16,14,12;设其平均数为 ,中位数为
,中位数为 ,众数为
,众数为 ,则有( )
,则有( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某大学对 名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这
名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这 名学生在该次自主招生水平测试中成绩不低于
名学生在该次自主招生水平测试中成绩不低于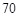 分的学生数是( )
分的学生数是( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果 服从正态分布
服从正态分布
 .若
.若 在(0,1)内取值的概率为0.4,则
在(0,1)内取值的概率为0.4,则 在(0,2)内取值的概率为0.8 ;
在(0,2)内取值的概率为0.8 ;
④对分类变量X与Y的随机变量K2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
其中真命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
为了调查城市PM2.5的情况,按地域把48个城市分成大型、中型、小型三组,对应的城市数分别为8,16,24.若用分层抽样的方法抽取12个城市,则中型组中应抽取的城市数为
| A.3 | B.4 | C.5 | D.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下图是两组各 名同学体重(单位:
名同学体重(单位: )数据的茎叶图.设
)数据的茎叶图.设 ,
, 两组数据的平均数依次为
两组数据的平均数依次为 和
和 ,标准差依次为
,标准差依次为 和
和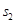 ,那么( )
,那么( )
(注:标准差 ,其中
,其中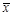 为
为 的平均数)
的平均数)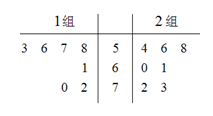
A. , , | B. , ,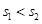 |
C. , ,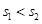 | D. , , |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号1,2,……,960,分组后在第一组采用简单随机抽样的方法抽到的号码为29,则抽到的32人中,编号落入区间 的人数为( )
的人数为( )
| A.10 | B.14 | C.15 | D.16 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:
①y与x负相关且 =2.347x-6.423;
=2.347x-6.423;
②y与x负相关且 =-3.476x+5.648;
=-3.476x+5.648;
③y与x正相关且 =5.437x+8.493;
=5.437x+8.493;
④y与x正相关且 =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正确的结论的序号是( )
| A.①② | B.②③ |
| C.③④ | D.①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com