练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （2012年高考（辽宁理））已知正三棱锥ABC,点P,A,B,C都在半径为的求面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为________.

     

    【解析】因为在正三棱锥ABC中,PA,PB,PC两两互相垂直,所以可以把该正三棱锥看作为一个正方体的一部分,(如图所示),此正方体内接于球,正方体的体对角线为球的直径,球心为正方体对角线的中点.

    球心到截面ABC的距离为球的半径减去正三棱锥ABC在面ABC上的

    高.已知球的半径为,所以正方体的棱长为2,可求得正三棱锥ABC在面ABC上的高为,所以球心到截面ABC的距离为

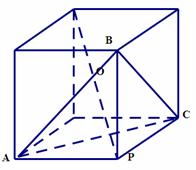
    【点评】本题主要考查组合体的位置关系、抽象概括能力、空间想象能力、运算求解能力以及转化思想,该题灵活性较强,难度较大.该题若直接利用三棱锥来考虑不宜入手,注意到条件中的垂直关系,把三棱锥转化为正方体来考虑就容易多了.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012年高考（辽宁理））若,则下列不等式恒成立的是（　　）

    A．     B．         

    C．   D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012年高考（辽宁理））已知等比数列为递增数列,且,则数列的通项公式______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012年高考（辽宁理））在长为12cm的线段AB上任取一点         C．现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为                       （　　）

    A．             B．             C．            D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012年高考（辽宁理））在中,角A、B、C的对边分别为a,b,c.角A,B,C成等差数列.

    (Ⅰ)求的值;

    (Ⅱ)边a,b,c成等比数列,求的值.

    查看答案和解析>>

    同步练习册答案