
| A. | p∨r | B. | p∧(¬q) | C. | (¬q)∧(¬r) | D. | (¬p)∧q |
分析 命题p:由方程x2+y2+ax+5=0化为:$(x+\frac{a}{2})^{2}$+y2=$\frac{{a}^{2}}{4}$-5表示一个圆,则$\frac{{a}^{2}}{4}$-5>0,a2>20,即可判断出命题的真假.
命题q:?x∈R,0.1x>0,∈[m,-m],可知:?m∈(-∞,0),方程0.1x+msinx=0总有实数解,即可判断出真假.
命题r:由m∈(1,3),则msinx+mcosx=m$\sqrt{2}$sin$(x+\frac{π}{4})$∈$(-\sqrt{2},3\sqrt{2})$<3$\sqrt{2}$,即可判断出真假.
解答 解:命题p:由方程x2+y2+ax+5=0化为:$(x+\frac{a}{2})^{2}$+y2=$\frac{{a}^{2}}{4}$-5表示一个圆,则$\frac{{a}^{2}}{4}$-5>0,a2>20,由a2≥20是方程x2+y2+ax+5=0表示一个圆的必要不充分条件,因此是假命题.
命题q:∵?x∈R,0.1x>0,-msinx∈[m,-m],可知:?m∈(-∞,0),方程0.1x+msinx=0总有实数解,是真命题.
命题r:若m∈(1,3),则msinx+mcosx=m$\sqrt{2}$sin$(x+\frac{π}{4})$∈$(-\sqrt{2},3\sqrt{2})$<3$\sqrt{2}$,因此r是假命题.
那么,下列命题为真命题的是:D.
故选:D.
点评 本题考查了简易逻辑的性质、函数的单调性、圆的标准方程、三角函数求值,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | b<c<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
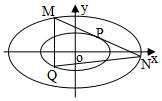 已知椭圆Cn:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n(a>b>0,n∈N*),F1、F2是椭圆C4的焦点,A(2,$\sqrt{2}$)是椭圆C4上一点,且$\overrightarrow{A{F}_{2}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0;
已知椭圆Cn:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n(a>b>0,n∈N*),F1、F2是椭圆C4的焦点,A(2,$\sqrt{2}$)是椭圆C4上一点,且$\overrightarrow{A{F}_{2}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | ±$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知ABCD是上、下底边长分别为2和6,高为$\sqrt{3}$的等腰梯形,将它沿对称轴OO1折成直二面角.
如图,已知ABCD是上、下底边长分别为2和6,高为$\sqrt{3}$的等腰梯形,将它沿对称轴OO1折成直二面角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com