分析:(Ⅰ)证明PO⊥底面ABCD,只需证明PO⊥AC,PO⊥BD;
(Ⅱ)建立空间直角坐标系,求出直线CP的方向向量,平面BDF的法向量,利用向量的夹角公式可求直线CP与平面BDF所成角的大小;
(Ⅲ)设
=λ(0≤λ≤1),若使CM∥平面BDF,需且仅需
•=0且CM?平面BDF,即可得出结论.
解答: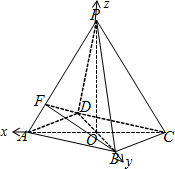
(Ⅰ)证明:因为底面ABCD是菱形,AC∩BD=O,
所以O为AC,BD中点.-------------------------------------(1分)
又因为PA=PC,PB=PD,
所以PO⊥AC,PO⊥BD,---------------------------------------(3分)
所以PO⊥底面ABCD.----------------------------------------(4分)
(Ⅱ)解:由底面ABCD是菱形可得AC⊥BD,
又由(Ⅰ)可知PO⊥AC,PO⊥BD.
如图,以O为原点建立空间直角坐标系O-xyz.
由△PAC是边长为2的等边三角形,
PB=PD=,
可得
PO=,OB=OD=.
所以
A(1,0,0),C(-1,0,0),B(0,,0),P(0,0,).---------------------------------------(5分)
所以
=(1,0,),
=(-1,0,).
由已知可得
=+=(,0,)-----------------------------------------(6分)
设平面BDF的法向量为
=(x,y,z),则
令x=1,则
z=-,所以
=(1,0,-
).----------------------------------------(8分)
因为cos
<,>==-
,----------------------------------------(9分)
所以直线CP与平面BDF所成角的正弦值为
,
所以直线CP与平面BDF所成角的大小为30°.-----------------------------------------(10分)
(Ⅲ)解:设
=λ(0≤λ≤1),则
=+=+λ=(1,(1-λ),λ).---------------------------------(11分)
若使CM∥平面BDF,需且仅需
•=0且CM?平面BDF,---------------------(12分)
解得
λ=∈[0,1],----------------------------------------(13分)
所以在线段PB上存在一点M,使得CM∥平面BDF.
此时
=
.-----------------------------------(14分)

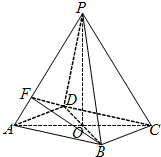 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD= (Ⅰ)证明:因为底面ABCD是菱形,AC∩BD=O,
(Ⅰ)证明:因为底面ABCD是菱形,AC∩BD=O,

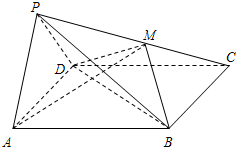 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.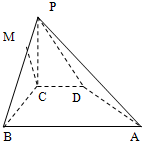 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB