
已知向量 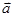 =(cos
=(cos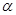 ,sin
,sin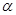 ),
),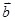 =(cos
=(cos ,sin
,sin ),
),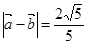 。
。
(1)求cos(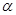 -
- )的值;
)的值;
(2)若0<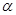 <
<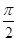 ,-
,-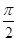 <
< <0,且sin
<0,且sin =-
=-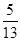 ,求sin
,求sin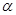 的值.
的值.
科目:高中数学 来源: 题型:解答题
设向量a=(2,sinθ),b=(1,cosθ),θ为锐角(1)若a·b=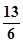 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+ )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)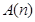 :
: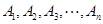 与
与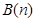 :
: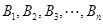 ,其中
,其中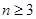 ,若同时满足:①两点列的起点和终点分别相同;②线段
,若同时满足:①两点列的起点和终点分别相同;②线段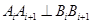 ,其中
,其中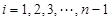 ,则称
,则称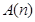 与
与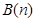 互为正交点列.
互为正交点列.
(1)求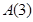 :
: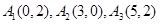 的正交点列
的正交点列 ;
;
(2)判断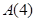 :
: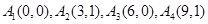 是否存在正交点列
是否存在正交点列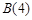 ?并说明理由;
?并说明理由;
(3)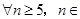 N,是否都存在无正交点列的有序整点列
N,是否都存在无正交点列的有序整点列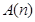 ?并证明你的结论.
?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com