圆x2+y2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离之差是 .
【答案】
分析:把圆的方程化为标准方程,找出圆心坐标和圆的半径,过圆心M作已知直线的垂线,与圆分别交于A和B点,垂足为C,由图形可知|AC|为圆上点到已知直线的最大距离,|BC|为圆上点到已知直线的最小距离,而|AC|-|BC|等于圆的直径,由圆的半径即可求出直径,即为最大距离与最小距离之差.
解答:解:把圆的方程化为标准方程得:(x-2)
2+(y-2)
2=18,
∴圆心M坐标为(2,2),半径|AM|=|BM|=3
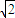
,
过M作出直线x+y-14=0的垂线,与圆M交于A、B两点,垂足为C,
如图所示:
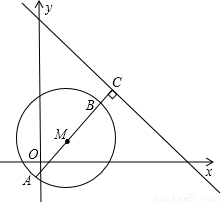
由图形可得|AC|为圆上点到直线x+y-14=0的最大距离,|BC|为圆上点到直线x+y-14=0的最小距离,
则最大距离与最小距离之差为|AC|-|BC|=|AB|=2|AM|=6
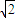
.
故答案为:6
 点评:
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,利用了数形结合的思想,其中找出|AC|为圆上点到直线x+y-14=0的最大距离,|BC|为圆上点到直线x+y-14=0的最小距离是解本题的关键.

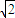 ,
,
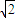 .
.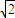


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案