
分析 (1)利用通项公式列出方程组,解出首项和公差,代入通项公式;
(2)解出bn的通项公式,使用分项法求出数列的和.
解答 解:(1)设{an}公差为d,则$\left\{\begin{array}{l}{{a}_{1}+d=5}\\{2{a}_{1}+4d=12}\end{array}\right.$,解得a1=4,d=1.∴an=4+n-1=n+3.
(2)bn=2n+n,设{bn}的前n项和为Sn,
∴Sn=2+1+22+2+23+3+24+4+…+2n+n=(2+22+23+…+2n)+(1+2+3+…+n)=$\frac{2(1-{2}^{n})}{1-2}$+$\frac{(1+n)n}{2}$=2n+1+$\frac{{n}^{2}+n}{2}$-2.
点评 本题考查了等差数列的通项公式,数列求和,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
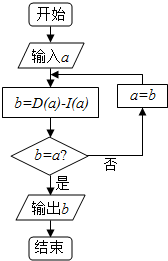 已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
已知集合A-{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )| A. | 792 | B. | 693 | C. | 594 | D. | 495 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com