
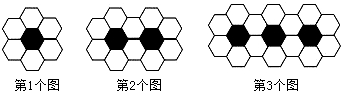
 用黑白两种正六边形瓷砖按如图所示规律拼成若干图案.
用黑白两种正六边形瓷砖按如图所示规律拼成若干图案.分析 (1)根据第1个图形有6块白色地面瓷砖,第2个图形有10块白色瓷砖,每多1个黑色瓷砖则多4块白色瓷砖,根据此规律即可写出第n个图案中的白色瓷砖的块数.
(2)第n-1个图案白色瓷砖的块数是:4(n-1)+2=4n-2,黑色瓷砖的块数是:n-1,可得第n-1个图案中黑色瓷砖和白色瓷砖的总块数.
解答 解:(1)第1个图案白色瓷砖的块数是:6,
第2个图案白色瓷砖的块数是:10=6+4,
第3个图案白色瓷砖的块数是:14=6+4×2,
…
以此类推,第n个图案白色瓷砖的块数是:6+4(n-1)=4n+2.
(2)第n-1个图案白色瓷砖的块数是:4(n-1)+2=4n-2,黑色瓷砖的块数是:n-1,
∴第n-1个图案中黑色瓷砖和白色瓷砖共有4n-3块
点评 本题考查了图形的变化问题的规律探寻,看出图形变化规律“每多一块黑色瓷砖则白色瓷砖增加4块”是解题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
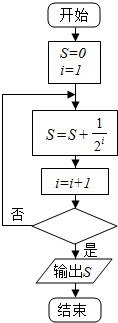 下图给出的是计算$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{10}}$的值的一个程序框图,其中判断框内应填入的条件是( )
下图给出的是计算$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{10}}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i≥10 | B. | i>11 | C. | i>10 | D. | i<11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
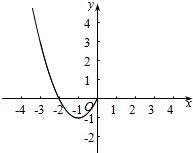 已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,
已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
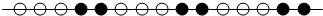
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com