
(本题15分)已知函数 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时,  .
.
(1)写出函数 的解析式;
的解析式;
(2)写出函数 的增区间;
的增区间;
(3)若函数 ,求函数
,求函数 的最小值
的最小值 .[来
.[来
(1) (2)
(2)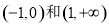 ,(3)
,(3)
【解析】
试题分析:(1)由函数的奇偶性求解析式时,要注意求那个区域内的解析式,就是变量在这个区域内;(2)求分段函数的单调性,可先求出各段单调性,然后一般用逗号连接; (3)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解题的关键是对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论;
试题解析:(1)当 时,
时,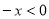 ,所以
,所以 ,函数
,函数 是定义在
是定义在 上的偶函数,所以
上的偶函数,所以 ,所以
,所以 ,
,
所以 .
.
(2)函数 ,当
,当 ,对称轴是直线
,对称轴是直线 ,在
,在 上单调递增;当
上单调递增;当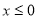 时,
时, ,对称轴
,对称轴 ,在
,在 单调递增,所以,函数的单调递增是
单调递增,所以,函数的单调递增是
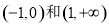
(3)①当 时,即
时,即

②当 时,即
时,即

③当 时,即
时,即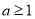

综上: .
.
考点:函数的奇偶性,单调性及最值.


科目:高中数学 来源:2015届内蒙古赤峰市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知函数f(x)=x2﹣alnx,a∈R.
(Ⅰ)当a=4时,求函数f(x)在[1,e]上的最小值及相应的x的值;
(Ⅱ)若存在x∈[2,e],使得f(x)≥(a﹣2)x成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高二上学期10月月考数学试卷(解析版) 题型:填空题
已知 :
: ,
, :
: ,则
,则 是
是 的_____________条件.
的_____________条件.
(在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选择一个填写)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高一上学期10月月考数学试卷(解析版) 题型:填空题
对于实数 ,定义运算
,定义运算 ,设函数
,设函数 ,若函数
,若函数 的图像与
的图像与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com