
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4及圆内一点P(2,5).
(1)求过P点的弦中,弦长最短的弦所在的直线方程;
(2)求过点M(5,0)与圆C相切的直线方程.
【答案】
解:(1)∵圆C:(x﹣3)2+(y﹣4)2=4及圆内一点P(2,5),
∴由题意,过P点且与CP垂直的弦长最短,
∵圆心C点坐标为(3,4),∴![]() ,
,
∴所求直线的斜率k=1,代入点斜式方程,
得y﹣5=x﹣2,即x﹣y+3=0.
∴P点的弦中,弦长最短的弦所在的直线方程为x﹣y+3=0.
(Ⅱ)当直线垂直x轴时,即x=5,圆心C到直线的距离为2,此时直线x=5与圆C相切,
当直线不垂直x轴时,设直线方程为y=k(x﹣5),即kx﹣y﹣5k=0,
圆心C到直线的距离d=![]()
解得k=-![]() ,
,
∴所求切线方程为3x+4y﹣15=0,或x=5.
【解析】(1)过P点且与CP垂直的弦长最短,由此能求出点的弦中,弦长最短的弦所在的直线方程.
(Ⅱ)当直线垂直x轴时,直线x=5与圆C相切,当直线不垂直x轴时,设直线方程kx﹣y﹣5k=0,由圆心C到直线的距离等于半径,能求出切线方程.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高0.02万元,已知建筑第5层楼房时,每平方米建筑费用为0.8万元.
(1)若学生宿舍建筑为![]() 层楼时,该楼房综合费用为
层楼时,该楼房综合费用为![]() 万元,综合费用是建筑费用与购地费用之和),写出
万元,综合费用是建筑费用与购地费用之和),写出![]() 的表达式;
的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
【答案】(1)![]() ;(2)学校应把楼层建成
;(2)学校应把楼层建成![]() 层,此时平均综合费用为每平方米
层,此时平均综合费用为每平方米![]() 万元
万元
【解析】
![]() 由已知求出第
由已知求出第![]() 层楼房每平方米建筑费用为
层楼房每平方米建筑费用为![]() 万元,得到第
万元,得到第![]() 层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高
层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高![]() 万元
万元![]() ,然后利用等差数列前
,然后利用等差数列前![]() 项和求建筑
项和求建筑![]() 层楼时的综合费用
层楼时的综合费用![]() ;
;
![]() 设楼房每平方米的平均综合费用为
设楼房每平方米的平均综合费用为![]() ,则
,则![]() ,然后利用基本不等式求最值.
,然后利用基本不等式求最值.
解:![]() 由建筑第5层楼房时,每平方米建筑费用为
由建筑第5层楼房时,每平方米建筑费用为![]() 万元,
万元,
且楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,
万元,
可得建筑第1层楼房每平方米建筑费用为:![]() 万元.
万元.
建筑第1层楼房建筑费用为:![]() 万元
万元![]() .
.
楼房每升高一层,整层楼建筑费用提高:![]() 万元
万元![]() .
.
建筑第x层楼时,该楼房综合费用为:![]() .
.
![]() ;
;
![]() 设该楼房每平方米的平均综合费用为
设该楼房每平方米的平均综合费用为![]() ,
,
则:![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立.
时,上式等号成立.
![]() 学校应把楼层建成10层,此时平均综合费用为每平方米
学校应把楼层建成10层,此时平均综合费用为每平方米![]() 万元.
万元.
【点睛】
本题考查简单的数学建模思想方法,训练了等差数列前n项和的求法,训练了利用基本不等式求最值,是中档题.
【题型】解答题
【结束】
20
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装店为庆祝开业“三周年”,举行为期六天的促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,第五天该服装店经理对前五天中参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 |
| 4 | 6 | 10 | 23 | 22 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)预测第六天的参加抽奖活动的人数(按四舍五入取到整数).
参考公式与参考数据: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P - ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
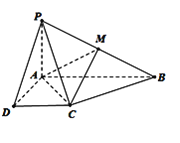
(1)证明平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年五一小长假,以洪崖洞、李子坝轻轨、长江索道、一棵树观景台为代表的网红景点,把重庆推上全国旅游人气搒的新高.外地客人小胖准备游览上面这![]() 个景点,他游览每一个景台的概率都是
个景点,他游览每一个景台的概率都是![]() ,且他是否游览哪个景点互不影响.设
,且他是否游览哪个景点互不影响.设![]() 表示小胖离开重庆时游览的景点数与没有游览的景点数之差的绝对值.
表示小胖离开重庆时游览的景点数与没有游览的景点数之差的绝对值.
(1)记“函数![]() 是实数集
是实数集![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 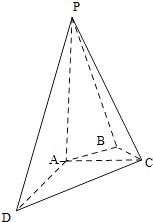
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com