
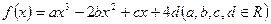 的图象关于原点对称,且
的图象关于原点对称,且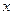 =1时,f(x)取极小值
=1时,f(x)取极小值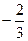 。
。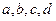 的值;
的值;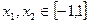 时,求证:
时,求证: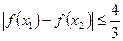 。
。 有f(-x)="-" f(x).
有f(-x)="-" f(x). . ∴f′(1)=0且f(1)="-"
. ∴f′(1)=0且f(1)="-"  ,
, +c=-
+c=- . 解得a=
. 解得a=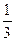 ,c=-1………………………………….6分
,c=-1………………………………….6分 , fmin(x)=f(1)= -
, fmin(x)=f(1)= - .
. .
. f(x1)-f(x2)|≤
f(x1)-f(x2)|≤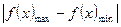 =
= +
+ =
=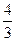 .
. ]时,|f(x1)-f(x2)|≤
]时,|f(x1)-f(x2)|≤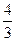 ………………………………………….12分
………………………………………….12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com