已知函数
，其中a∈R，
（Ⅰ）若a=0，求函数f（x）的定义域和极值；
（Ⅱ）当a=1时，试确定函数
的零点个数，并证明.
（Ⅰ）
且
；函数
有极小值
;（Ⅱ）函数
存在两个零点.
【解析】
试题分析：（Ⅰ）由分母不为0，求出函数的定义域，利用导数的正负性，求出函数的单调区间，从而求出极值；（Ⅱ）利用导数求出函数的单调区间，知函数是先增后减再增的，又极大值为0，极小值小于0，从而判断函数有两面个零点.
试题解析：【解析】
（Ⅰ）函数
的定义域为且， 2分
．令
，得
．当
变化时，
和
的变化情况如下：
|
|
|
|
|
| － | － |
| ＋ |
| ↘ | ↘ | 极小 | ↗ |
所以的单调减区间为
，
；单调增区间
．
故当
时，函数有极小值. 5分
（Ⅱ）结论：函数
存在两个零点．证明过程如下：由题意，函数
．
因为
．所以函数的定义域为
．求导，得
， 7分
令
，得
，
，当
变化时，和
的变化情况如下：
|
|
|
|
|
|
|
|
| — |
|
|
|
| 极大 | ↘ | 极小 | ↗ |
故函数的单调减区间为
；单调增区间为
，
．
当时，函数有极大值
；
当
时，函数有极小值
. 10分
因为函数在单调递增，且，所以对于任意
，
.
因为函数在
单调递减，且，所以对于任意
，.
因为函数在单调递增，且
，
，
所以函数在上存在唯一
，使得
，
故函数存在两个零点（即
和
）. 12分.
考点：1.利用导数研究函数的极值；2.函数的定义域及其求法．
科目：高中数学 来源：2015届河南省名校高三上学期期中理科数学试卷（解析版） 题型：解答题
已知函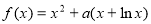数
，
，
是常数．
（1）求函数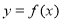
的图象在点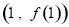
处的切线方程；
（2）若函数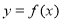图象上的点都在第一象限，试求常数
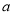的取值范围；
（3）证明：
，存在
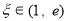，使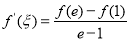
．
查看答案和解析>>
科目：高中数学 来源：2015届河南省名校高三上学期期中文科数学试卷（解析版） 题型：选择题
已知集合
，
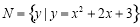，则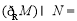
（ ）
A．{x|10＜x＜1} B．{x|x＞1} C．{x|x≥2} D．{x|1＜x＜2}
查看答案和解析>>
科目：高中数学 来源：2015届河南省八校高三上学期第一次联考理科数学试卷（解析版） 题型：选择题
在△ABC中，内角A,B,C的对边分别为a，b，c，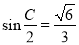
,a=b=3，点P是边AB上的一个三等分点，则
=( )
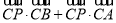A.0 B.6 C.9 D.12
查看答案和解析>>
科目：高中数学 来源：2015届河南省八校高三上学期第一次联考文科数学试卷（解析版） 题型：填空题
已知下列5个命题，其中正确的命题____（写出所有正确命题的代号）
①函数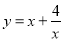
，x∈[1,4]的最大值是4.
②底面直径和高都是2的圆柱侧面积，等于内切球的表面积;
③在抽样过程，三种抽样方法抽取样本时，每个个体被抽取的可能性不相等；
④
是椭圆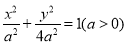
的两个焦点，过
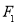点的弦
,
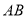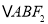的周长是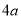
；
⑤“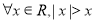
”的否定，“
”
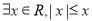查看答案和解析>>
科目：高中数学 来源：2015届河北省邯郸市高三上学期摸底考试理科数学试卷（解析版） 题型：解答题
已知椭圆C：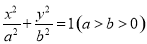
的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线
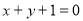与以椭圆C的右焦点为圆心，以椭圆的长半轴长为半径的圆相切．
（1）求椭圆的方程．
（2）设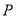
为椭圆上一点，若过点
的直线
与椭圆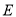
相交于不同的两点
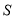和
,且满足
（O为坐标原点），求实数
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
↗
，其中t∈（0，π），则t=( )
B.
C.
D.
，则（ ）
B.
C.
D.
，
为
的等差数列，则
_____________．