
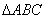 中内角
中内角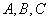 的对边分别为
的对边分别为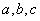 ,向量
,向量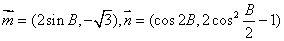 且
且
(Ⅰ)求锐角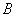 的大小,
的大小,
(Ⅱ)如果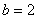 ,求
,求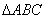 的面积
的面积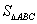 的最大值
的最大值
思路点拨:(Ⅰ)问利用平行向量的坐标运算将向量知识转化为三角函数,利用三角恒
等变换知识解决;(Ⅱ)问利用余弦定理与基本不等式结合三角形面积公式解决。
解:(1)
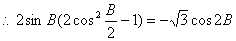
 即
即  ……………3分
……………3分
又 为锐角
为锐角


 ……………………………………6分
……………………………………6分
(2) 由余弦定理得
由余弦定理得
即
 ----------------------------------------------------------9
----------------------------------------------------------9
又 代入上式得
代入上式得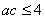 (当且仅当
(当且仅当
 时等号成立)…10分
时等号成立)…10分
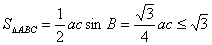 (当且仅当
(当且仅当  时等号成立。)………12分
时等号成立。)………12分
名师语:本题将三角函数、向量与解三角形有机的结合在一起,题目新颖而又精巧,既符合在知识“交汇点”处构题,又能加强对双基的考查,特别是向量的坐标表示及运算,大大简化了向量的数量积的运算,该类问题的解题思路通常是将向量的数量积用坐标运算后转化为三角函数问题,然后用三角函数基本公式结合正、余弦定理求解。


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:2014届辽宁省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)
在 中内角
中内角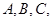 的对边分别为
的对边分别为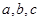 ,且
,且
(1)求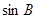 的值;
的值;
(2)如果b=4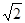 ,且a=c,求
,且a=c,求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省高二上学期期中考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
在 中内角
中内角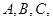 的对边分别为
的对边分别为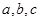 ,且
,且
(1)求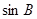 的值;
的值;
(2)如果b=4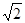 ,且a=c,求
,且a=c,求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省、黄石二中高三上学期联考考试理科数学卷 题型:解答题
(本题满分12分)
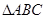 中内角
中内角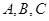 的对边分别为
的对边分别为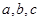 ,
,
向量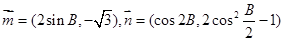 且
且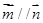
(Ⅰ)求锐角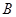 的大小,
的大小,
(Ⅱ)如果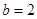 ,求
,求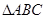 的面积
的面积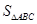 的最大值
的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com