
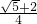


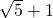
 ),则把四边形ABCP的面积表示成三角函数形式;然后利用三角函数的有关公式(特别是asinx+bcosx=
),则把四边形ABCP的面积表示成三角函数形式;然后利用三角函数的有关公式(特别是asinx+bcosx= sin(x+φ)),把其转化为正弦型函数;最后根据正弦函数的值域,求得四边形ABCP面积的最大值.
sin(x+φ)),把其转化为正弦型函数;最后根据正弦函数的值域,求得四边形ABCP面积的最大值. 解:据题意画图如下
解:据题意画图如下 ).
).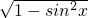 =cosx
=cosx sinxcosx=
sinxcosx= (1-cos2x)+
(1-cos2x)+ sin2x
sin2x sin2x-
sin2x- cos2x)+
cos2x)+ =
= sin(2x-φ)+
sin(2x-φ)+
 +
+ ,即
,即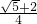 .
.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,将正方形ABCD沿对角线BD折成直二面角,连接A′C得到三棱锥A′-BCD,A′F 垂直BD于F,E为BC的中点.
如图,将正方形ABCD沿对角线BD折成直二面角,连接A′C得到三棱锥A′-BCD,A′F 垂直BD于F,E为BC的中点.查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修二4.2直线、圆的位置关系练习卷(三) 题型:解答题
设正方形ABCD的外接圆方程为x2+y2–6x+a=0(a<9),C、D点所在直线l的斜率为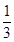 ,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高一下学期期中数学试卷(解析版) 题型:解答题
如图所示,圆柱的高为2,底面半径为 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
.
(1)求证: ;
;
(2)若四边形ABCD是正方形,求证 ;
;
(3)在(2)的条件下,求二面角A-BC-E的平面角的一个三角函数值。

【解析】第一问中,利用由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF
第二问中,由线面垂直得到线线垂直。四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



第三问中,设正方形ABCD的边长为x,则在
在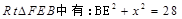

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
证明:(1)由圆柱的性质知:AD平行平面BCFE
又过 作圆柱的截面交下底面于
作圆柱的截面交下底面于 .
. ∥
∥
又AE、DF是圆柱的两条母线
 ∥DF,且AE=DF
∥DF,且AE=DF  AD∥EF
AD∥EF

(2) 四边形ABCD是正方形
四边形ABCD是正方形
 又
又
BC、AE是平面ABE内两条相交直线



(3)设正方形ABCD的边长为x,则在
在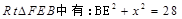

由(2)可知: 为二面角A-BC-E的平面角,所以
为二面角A-BC-E的平面角,所以
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com