某进修学校为全市教师提供心理学和计算机两个项目的培训,以促进教师的专业发展,每位教师可以选择参一项培训、参加两项培训或不参加培.现知垒市教师中,选择心理学培训的教师有60%,选择计算机培训的教师有75%,每位教师对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(1)任选1名教师,求该教师选择只参加一项培训的概率;
(2)任选3名教师,记ξ为3人中选择不参加培训的人数,求ξ的分布列和期望.
【答案】
分析:(1)任选1名教师,记“该教师选择心理学培训”为事件A,“该教师选择计算机培训”为事件B,由已知可得两事件发生的概率,从中任取一项的概率即为

(2)因为每个人的选择是相互独立的,所以3人中选择不参加培训的人数ξ服从二项分布,列出ξ的分布列,代入数学期望公式,可得答案.
解答:解:(1)任选1名教师,记“该教师选择心理学培训”为事件A,“该教师选择计算机培训”为事件B,
由题设知,事件A与B相互独立,且P(A)=0.6,P(B)=0.75. …(1分)(1)
任选1名,该教师只选择参加一项培训的概率是
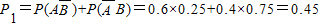
…(4分)
(2)任选1名教师,该人选择不参加培训的概率是

. …(5分)
因为每个人的选择是相互独立的,
所以3人中选择不参加培训的人数ξ服从二项分布B(3,0.1),…(6分)
且
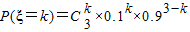
,k=0,1,2,3,…(8分)
即ξ的分布列是
| ξ | | 1 | 2 | 3 |
| P | 0.729 | 0.243 | 0.027 | 0.001 |
…(10分)
所以,ξ的期望是Eξ=1×0.243+2×0.027+3×0.001=0.3. …(12分)
(或ξ的期望是Eξ=3×0.1=0.3.)
点评:本题考查的知识点是随机变量及其分布列,相互独立事件的概率乘法公式,离散型随机变量的期望,熟练掌握随机变量及其分布列及数学期望的求解步骤是解答的关键.


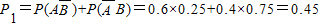 …(4分)
…(4分) . …(5分)
. …(5分)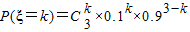 ,k=0,1,2,3,…(8分)
,k=0,1,2,3,…(8分)

 口算能手系列答案
口算能手系列答案