
科目:高中数学 来源:2014-2015学年浙江省等三校高二上学期期中考试数学试卷(解析版) 题型:填空题
数列{an}的前n项和为Sn,且Sn=n2-n(n∈N*),则通项an=________.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省宜昌市高一上学期期中考试数学试卷(解析版) 题型:解答题
若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0,满足f =f(x)-f(y).
=f(x)-f(y).
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+3)-f <2.
<2.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年福建厦门双十中学高二上期中文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数 ,且不等式
,且不等式 的解集为
的解集为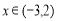 ;
;
(1)求函数 的解析式;
的解析式;
(2)c为何值时,关于 的不等式
的不等式 无解.
无解.
查看答案和解析>>
科目:高中数学 来源:2016届重庆市高三上学期期中文科数学试卷(解析版) 题型:选择题
设 是定义域在
是定义域在 上的偶函数,对
上的偶函数,对 ,都有
,都有 且当
且当 时,
时, ,若在区间
,若在区间 内关于
内关于 的方程
的方程 至少有两个不同的实数根,至多有3个不同的实数根,则
至少有两个不同的实数根,至多有3个不同的实数根,则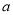 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中文科数学试卷(解析版) 题型:填空题
设 是定义在
是定义在 上的偶函数,对
上的偶函数,对 ,都有
,都有 ,且当
,且当 时,
时,  .若在区间
.若在区间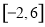 内关于
内关于 的方程
的方程 恰有3个不同实根,则
恰有3个不同实根,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
【答案】A
【解析】
试题分析:由 ,得
,得 ,所以函数
,所以函数 是周期为4的函数.又
是周期为4的函数.又 是偶函数,且
是偶函数,且 时,
时, =
= ,所以
,所以 时,
时, .方程
.方程
 在
在 内有三个根,即函数
内有三个根,即函数 与函数
与函数
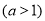 在
在 内有三个交点,作出函数
内有三个交点,作出函数 与
与
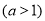 图像如图所示,则两个图像在
图像如图所示,则两个图像在 内恰有三个交点的条件是
内恰有三个交点的条件是 ,解得
,解得 ,故选B.
,故选B.

考点:1、指数函数与对数函数的图象与性质;2、函数的零点与方程根的关系;3、不等式的解法.
【方法点睛】方程的根为对应函数的零点,而函数的零点通常还可转化为两个函数的交点,因此求解函数的零点个数通常有两种方法:(1)直接法,即求解出所有的零点;(2)数形结合法,即转化为原函数的图象与 轴的交点个数或分解为两个函数相等,进而判断两个函数图象的交点个数,此法往往更实用.而函数函数的图象要求正确,特别是关键点的作法.
轴的交点个数或分解为两个函数相等,进而判断两个函数图象的交点个数,此法往往更实用.而函数函数的图象要求正确,特别是关键点的作法.
【题型】选择题
【适用】较难
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
设 ,
,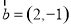 ,若
,若 ,则
,则 = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com