
分析 可画出图形,分别过B,D作AC的垂线BE,DF,从而根据条件可以求出$BE=DF=\frac{12}{5},AE=CF=\frac{9}{5}$,并且可得到DF⊥BE,从而可得到$\overrightarrow{AB}•\overrightarrow{CD}=(\overrightarrow{AE}+\overrightarrow{EB})•(\overrightarrow{CF}+\overrightarrow{FD})$,这样进行数量积的运算便可求出$\overrightarrow{AB}•\overrightarrow{CD}$的值,从而根据向量夹角的余弦公式可以求出cos$<\overrightarrow{AB},\overrightarrow{CD}>$,这样便可得出直线AB与直线CD所成角的余弦值.
解答  解:如图,
解:如图,
作BE⊥AC,垂足为E,作DF⊥AC,垂足为F;
根据条件AC=5,$BE=DF=\frac{12}{5}$,$AE=CF=\frac{9}{5}$;
二面角B-AC-D为直二面角;
∴DF⊥平面ABC;
∴DF⊥BE;
∴$\overrightarrow{AB}•\overrightarrow{CD}=(\overrightarrow{AE}+\overrightarrow{EB})•(\overrightarrow{CF}+\overrightarrow{FD})$=$\overrightarrow{AE}•\overrightarrow{CF}+\overrightarrow{AE}•\overrightarrow{FD}+\overrightarrow{EB}•\overrightarrow{CF}+\overrightarrow{EB}•\overrightarrow{FD}=-\frac{81}{25}+0+0+0=-\frac{81}{25}$;
∴$cos<\overrightarrow{AB},\overrightarrow{CD}>=\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{AB}||\overrightarrow{CD}|}$=$\frac{-\frac{81}{25}}{9}=-\frac{9}{25}$;
∴直线AB与直线CD所成角的余弦值为$\frac{9}{25}$.
故答案为:$\frac{9}{25}$.
点评 考查直角三角形边的关系,三角形的面积公式,直二面角的概念,面面垂直的性质定理,以及向量加法的几何意义,向量数量积的运算及计算公式,向量夹角的余弦的计算公式,弄清异面直线的所成角和异面直线的方向向量夹角的关系.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
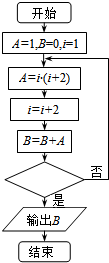 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )| A. | i≥13? | B. | i>14? | C. | i≥14? | D. | i≥15? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com