
分析 先分离参数a得$\frac{1}{a}$=xlnx,并构造函数f(x)=xlnx,再运用导数求出函数的单调区间,从而确定函数的值域,由此得出a的取值范围.
解答 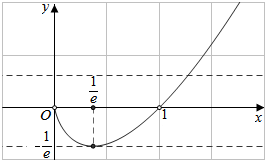 解:对于方程方程$\frac{1}{lnx}$-ax=0,其中x∈(0,1)∪(1,+∞),
解:对于方程方程$\frac{1}{lnx}$-ax=0,其中x∈(0,1)∪(1,+∞),
再分离参数a得,$\frac{1}{a}$=xlnx,记f(x)=xlnx,
则令f'(x)=1+lnx=0,解得,x=$\frac{1}{e}$,
当x∈(0,$\frac{1}{e}$)时,f'(x)<0;x∈($\frac{1}{e}$,+∞)时,f'(x)>0,
所以,f(x)先减后增,在x=$\frac{1}{e}$处取得极小值,也是函数的最小值,
即f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$,所以,f(x)的值域为(-$\frac{1}{e}$,+∞),
又∵x→0时,F(x)→0,如右图,
∴要使原方程只有一个实根,则$\frac{1}{a}$∈(0,+∞)∪{-$\frac{1}{e}$},
解得,a∈(0,+∞)∪{-e},
故答案为:(0,+∞)∪{-e}.
点评 本题主要考查了根的存在性和根的个数的判断,涉及导数在求函数的单调性和最值中的应用,体现了数形结合的解题思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
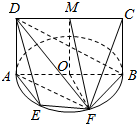 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com