Question

如图，在矩形ABCD中，AB＝2，BC＝a，△PAD为等边三角形，又平面PAD⊥平面ABCD.

(1)若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；

(2)当边BC上存在唯一点Q，使PQ⊥QD时，求二面角A－PD－Q的余弦值.

Answer 1

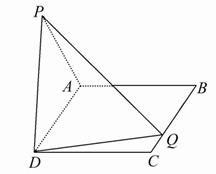
(1)取AD中点O，连接PO，则PO⊥AD

∵平面PAD⊥平面ABCD，

平面PAD∩平面ABCD＝AD，

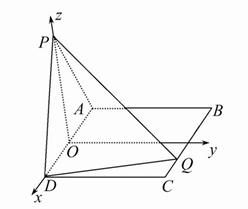
∴PO⊥平面ABCD.建立如图的空间直角坐标系，

则P(0,0，a)，D(，0,0).

设Q(t,2,0)，

则＝(t,2，－a)，＝(t－，2,0).

∵PQ⊥QD，

∴·＝t(t－)＋4＝0.

∴a＝2(t＋)，∵a>0，∴t>0，∴2(t＋)≥8，等号成立当且仅当t＝2.

故a的取值范围为[8，＋∞).

(2)由(1)知，当t＝2，a＝8时，边BC上存在唯一点Q，使PQ⊥QD.

此时Q(2,2,0)，D(4,0,0)，P(0,0,4).

设n＝(x，y，z)是平面PQD的法向量，

＝(2,2，－4)，＝(－2,2,0).

由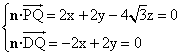

得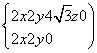

令x＝y＝3，则n＝(3,3，)是平面PQD的一个法向量.

而＝(0,2,0)是平面PAD的一个法向量，

设二面角A－PD－Q为θ，

由cosθ＝|cos〈，n〉|＝.

∴二面角A－PD－Q的余弦值为.