
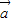 •
•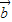 |=|
|=|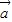 |•|
|•|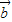 |,则
|,则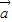 ∥
∥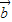 ;
;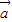 =(-1,1)在
=(-1,1)在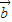 =(3,4)方向上的投影为
=(3,4)方向上的投影为 ;
;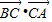 =20;
=20;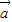 、
、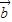 满足|
满足|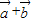 |=|
|=|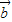 |,则|2
|,则|2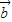 |>|
|>|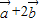 |.
|.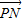 =
= (
(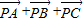 )则向量λ(
)则向量λ(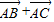 )(λ≠0)所在直线必过N点.其中所有真命题的序号是 .
)(λ≠0)所在直线必过N点.其中所有真命题的序号是 . 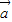 •
•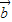 |=|
|=|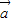 |•|
|•|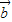 |,知cos<
|,知cos<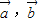 >=±1,由此能判断①的正误;
>=±1,由此能判断①的正误;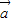 =(-1,1)在
=(-1,1)在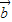 =(3,4)方向上的投影为|
=(3,4)方向上的投影为|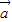 |•cos<
|•cos<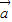 ,
,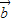 >,由此能判断②的正误;
>,由此能判断②的正误; ,由
,由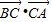 =|
=|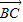 |•|
|•|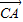 |•(-cos∠ACB)能求出结果;
|•(-cos∠ACB)能求出结果;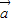 +2
+2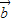 |=|
|=|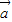 +
+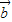 +
+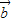 |≤|
|≤|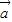 +
+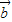 |+|
|+|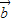 |=2|
|=2|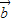 |,能推导出|2
|,能推导出|2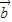 |>|
|>|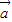 +2
+2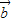 |;
|;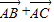 )(λ≠0)所在直线不一定过N点.
)(λ≠0)所在直线不一定过N点.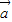 •
•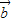 |=|
|=|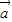 |•|
|•|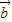 |,则cos<
|,则cos<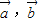 >=±1,
>=±1,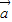 ∥
∥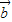 ,故①正确;
,故①正确;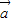 =(-1,1)在
=(-1,1)在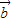 =(3,4)方向上的投影为|
=(3,4)方向上的投影为|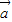 |•cos<
|•cos<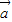 ,
,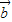 >=
>=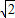 ×
×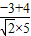 =
= ,故②正确;
,故②正确;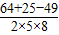 =
= ,
,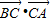 =|
=|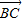 |•|
|•|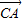 |•(-cos∠ACB)=5×8×(-
|•(-cos∠ACB)=5×8×(- )=-20,故③不正确;
)=-20,故③不正确;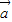 +2
+2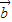 |=|
|=|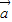 +
+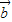 +
+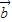 |≤|
|≤|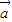 +
+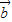 |+|
|+|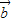 |=2|
|=2|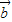 |,
|,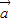 ,
,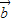 是非零向量,
是非零向量,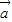 +
+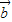 ≠
≠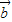 ,
,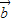 |>|
|>|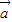 +2
+2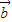 |,故④正确;
|,故④正确;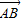 +
+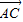 )=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),
)=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),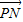 =
= (
(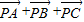 ),
), (8-3x,6-3y)=(
(8-3x,6-3y)=( -x,2-y),
-x,2-y), ,2).
,2).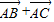 )(λ≠0)所在直线不一定过N点,故⑤不正确.
)(λ≠0)所在直线不一定过N点,故⑤不正确.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+1 |
查看答案和解析>>
科目:高中数学 来源:山西省山大附中2010-2011学年高二3月月考数学理科试题 题型:013
给出以下命题:(1)若![]() ,则f(x)>0;(2)
,则f(x)>0;(2)![]() ;(3)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
;(3)f(x)的原函数为F(x),且F(x)是以T为周期的函数,则![]() ;其中正确命题的个数为
;其中正确命题的个数为
0
1
2
3
查看答案和解析>>
科目:高中数学 来源:山西省康杰中学2011-2012学年高二下学期期中考试数学理科试题 题型:013
给出以下命题:
(1)若![]() ,则f(x)>0;
,则f(x)>0;
(2)![]() ;
;
(3)0比-i大
(4)两个复数互为共轭复数,当且仅当其和为实数
(5)x+yi=1+i的充要条件为x=y=1
(6)如果让实数a与ai对应,那么实数集与纯虚数集一一对应,
其中正确的命题个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com