
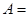 “三个点数都不相同”,
“三个点数都不相同”,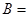 “至少出现一个
“至少出现一个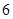 点”,则概率
点”,则概率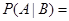 ( )
( )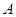 、
、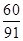
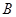 、
、
 、
、
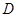 、
、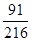
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:不详 题型:单选题
| A.A与B是互斥而非对立事件 | B.A与B是对立事件 |
| C.B与C是互斥而非对立事件 | D.B与C是对立事件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
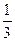 ,且面试是否合格互不影响,求:(1)至少有1人面试合格的概率;(2)签约人数X的分布列及数学期望。
,且面试是否合格互不影响,求:(1)至少有1人面试合格的概率;(2)签约人数X的分布列及数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
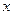 的不等式
的不等式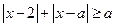 在
在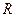 上恒成立,则
上恒成立,则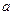 的最大值是1;
的最大值是1;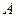 :“甲、乙中至少一人击中目标”与事件
:“甲、乙中至少一人击中目标”与事件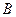 :“甲,乙都没有击中目标”是相互独立事件。
:“甲,乙都没有击中目标”是相互独立事件。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
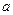 万元,年利率为
万元,年利率为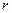 ,按复利计算,从2011年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为 万元.
,按复利计算,从2011年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为 万元.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com