
如图,在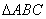 中,已知
中,已知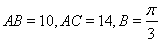 ,
,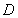 是
是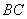 边上的一点,
边上的一点,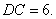
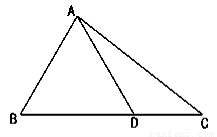
(Ⅰ)求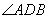 的值;
的值;
(Ⅱ)求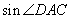 的值。
的值。
(1)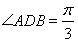 ;(2)
;(2)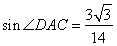 .
.
【解析】
试题分析:本题主要考查解三角形中的正弦定理、余弦定理的应用,考查基本的运算能力,考查分析问题解决问题的能力.法一:第一问,在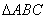 中利用余弦定理求边
中利用余弦定理求边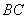 的长,利用
的长,利用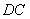 的长度,可以求出
的长度,可以求出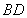 的长,通过
的长,通过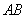 ,
,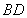 ,角
,角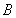 可以判断出
可以判断出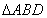 为等边三角形,所以
为等边三角形,所以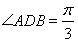 ,
,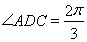 ,
,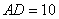 ;第二问,在
;第二问,在 中,利用余弦定理,可以求出
中,利用余弦定理,可以求出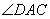 的余弦,再利用平方关系求出
的余弦,再利用平方关系求出 ;法二:第一问,在
;法二:第一问,在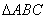 中利用正弦定理求出
中利用正弦定理求出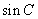 ,从而利用平方关系求出
,从而利用平方关系求出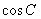 ,在
,在 中,利用余弦定理求出
中,利用余弦定理求出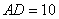 ,再确定
,再确定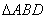 为等比三角形,从而得到
为等比三角形,从而得到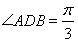 ,
,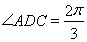 ;第二问,在
;第二问,在 中,再利用正弦定理求出
中,再利用正弦定理求出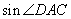 的值.
的值.
试题解析:法一:(Ⅰ)由余弦定理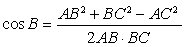
得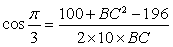 ,
,
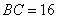 或
或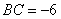 (舍去),
(舍去),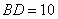 ,
,
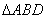 为等边三角形,
为等边三角形,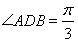 ,
,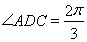 , 8分
, 8分
(Ⅱ)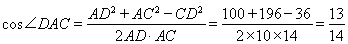 得
得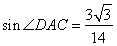 12分
12分
法二:(Ⅰ)由正弦定理可得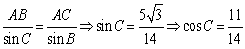
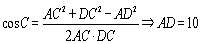 ,
,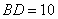 ,
,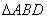 为等比三角形,
为等比三角形,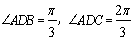 8分
8分
(Ⅱ)由正弦定理可得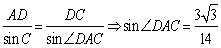 12分
12分
考点:1.余弦定理;2.正弦定理;3.平方关系.


科目:高中数学 来源: 题型:
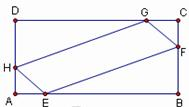 如图,在中,已知AB=2,BC=1,在AB、AD、CB、CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
如图,在中,已知AB=2,BC=1,在AB、AD、CB、CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
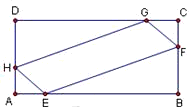 如图,在中,已知AB=2,BC=1,在AB、AD、CB、CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.
如图,在中,已知AB=2,BC=1,在AB、AD、CB、CD上,分别截取AE=AH=CF=CG=x(x>0),设四边形EFGH的面积为y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com