
分析 由题意可得$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$=$\frac{1}{2}$[(a+b)+(b+c)+(c+a)]($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$),再由三元基本不等式,即可得到最小值.
解答 解:由正数a、b、c满足a+b+c=1,
可得2=(a+b)+(b+c)+(c+a),
即有$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$=$\frac{1}{2}$[(a+b)+(b+c)+(c+a)]($\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$)
≥$\frac{1}{2}$•3$\root{3}{(a+b)(b+c)(c+a)}$•3$\root{3}{\frac{1}{a+b}•\frac{1}{b+c}•\frac{1}{c+a}}$=$\frac{9}{2}$,
当且仅当a=b=c=$\frac{1}{3}$时,取得最小值$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查基本不等式的运用:求最值,考查乘1法和化简运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?
如图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m,则每间羊圈的长和宽各为多少时,羊圈面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
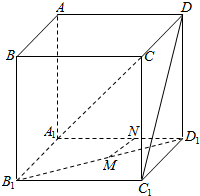 在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.
在正方体ABCD-A1B1C1D1中,若M、N分别为B1D1与C1D上的点,且MN⊥B1D,MN⊥C1D1,则MN与A1C的位置关系是MN∥A1C.1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7π}{10}$ | B. | $\frac{5π}{12}$ | C. | $\frac{7π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com