分析:(I)先求出函数的导数,f(x)在R上单调等价于x2+(a+2)x+a+2≥0恒成立,下面只要二次函数的根的判别式△≤0即可求得a的取值范围;
(Ⅱ)利用导数研究函数的极小值.先求出在函数的导数,再结合导数值为0求出极值点,最后结合函数的单调性即可求得函数f(x)的极小值.
解答:解:f′(x)=e
x[x
2+(a+2)x+a+2]
(Ⅰ)f′(x)=e
x[x
2+(a+2)x+a+2],
考虑到e
x>0恒成立且x
2系数为正,
∴f(x)在R上单调等价于x
2+(a+2)x+a+2≥0恒成立.
∴(a+2)
2-4(a+2)≤0,
∴-2≤a≤2,即a的取值范围是[-2,2],(8分)
(若得a的取值范围是(-2,2),可扣1分)
(Ⅱ)当
a=-时,
f(x)=(x2-x+2)ex,
f′(x)=ex(x2-x-),(10分)
令f′(x)=0,得
x=-,或x=1??,
令f′(x)>0,得
x<-,或x>1??,
令f′(x)<0,得
-<x<1??(12分)
x,f′(x),f(x)的变化情况如下表
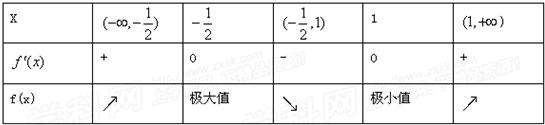
所以,函数f(x)的极小值为f(1)=
e(14分)
点评:本小题主要考查利用导数研究函数的单调性、利用导数研究函数的极值等基础知识,考查运算求解能力.属于基础题.



