
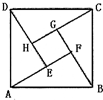
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是 ,求角θ的正切值.
,求角θ的正切值.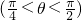 ,AB=1,EF=
,AB=1,EF= ,
, (S正方形ABCD-S正方形EFGH)=
(S正方形ABCD-S正方形EFGH)= (1-
(1- )=
)=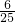 ,
, AF•BF=
AF•BF= sinθcosθ,
sinθcosθ, sinθcosθ=
sinθcosθ=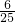 ,
,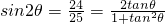 ,
,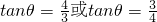 (θ为较大的锐角,不合题意,舍去)(10分)
(θ为较大的锐角,不合题意,舍去)(10分)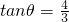 .(12分)
.(12分)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
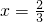 时,函数f(x)有极值,求函数f(x)的解析式;
时,函数f(x)有极值,求函数f(x)的解析式;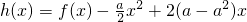 ,求h(x)的单调递增区间(其中a∈R).
,求h(x)的单调递增区间(其中a∈R).查看答案和解析>>
科目:高中数学 来源: 题型:单选题
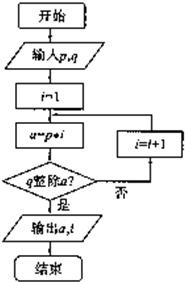 阅读如图所示的程序框图,若输入p=5,q=6,则输出a,i的值分别为
阅读如图所示的程序框图,若输入p=5,q=6,则输出a,i的值分别为查看答案和解析>>
科目:高中数学 来源: 题型:解答题
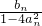 ,且点P1的坐标为(1,-1).
,且点P1的坐标为(1,-1).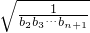 成立的最大实数k的值.
成立的最大实数k的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
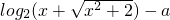 为奇函数,则a=
为奇函数,则a=
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
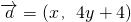 ,向量
,向量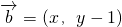 ,且
,且 ,动点M(x,y)的轨迹为E,
,动点M(x,y)的轨迹为E,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com