
【题目】从![]() 中这
中这![]() 个数中取
个数中取![]() 个数组成递增等差数列,所有可能的递增等差数列这个数记为
个数组成递增等差数列,所有可能的递增等差数列这个数记为![]() .
.
(1)当![]() 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及![]() 的值;
的值;
(2)求![]() ;
;
(3)求证:![]() .
.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)通过列举,可知符合要求的递增等差数列为![]() 共
共![]() 个.所以
个.所以![]() ;(2)由于
;(2)由于![]() ,且
,且![]() ,即有
,即有![]() 项,所以
项,所以![]() ,故
,故![]() 取
取![]() ,
,![]() 取
取![]() 个,归纳出个数
个,归纳出个数![]() ;(3)由于
;(3)由于![]() ,按照(2)的方法,求出
,按照(2)的方法,求出![]() 的表达式,然后利用差比较法证明不等式.
的表达式,然后利用差比较法证明不等式.
试题解析:
(1) 符合要求的递增等差数列为![]() 共
共![]() 个.
个.![]() .
.
(2)设满足条件的一个等差数列首项为![]() ,公差为
,公差为![]() 的可能取值为
的可能取值为![]() .对于给定的
.对于给定的
![]() ,当
,当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个(如:
个(如: ![]() 时,
时,![]() ,当
,当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个:
个: ![]() ,其它同理)
,其它同理)![]() 当
当![]() 取
取![]() 时,可得符合要求的等差数列个数为:
时,可得符合要求的等差数列个数为:![]() .
.
(3)证明: 设等差数列首项为![]() ,公差为
,公差为![]() ,记
,记![]() 的整数部分是
的整数部分是![]() ,则
,则![]() ,即
,即![]() .
.![]() 的可能取值为
的可能取值为![]() ,对于给定的
,对于给定的![]() , 当
, 当![]() 分别取
分别取![]() 时,可得递增等差数列
时,可得递增等差数列![]() 个.
个.![]() 当
当![]() 取
取![]() 时,符合要求的等差数列个数
时,符合要求的等差数列个数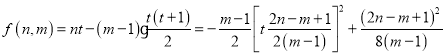 .由题意
.由题意![]() .又
.又 ,
,
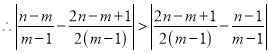 .
.
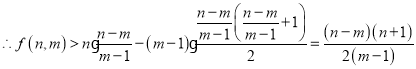 . 即
. 即![]() .
.


科目:高中数学 来源: 题型:
【题目】某商场预计全年分批购入每台2000元的电视机共3600台.每批都购入![]() 台(
台(![]() 是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线l:y=kx+![]() 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程__________.
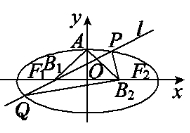
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y﹣1=0,l2:2x+ny+5=0,l3:mx+3y+1=0,若l1∥l2且l1⊥l3,则m+n的值为( )
A.﹣10B.﹣2C.2D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() 三个数中任取的一个数,求
三个数中任取的一个数,求![]() 不为空集的概率;
不为空集的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 不为空集的概率.
不为空集的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com