
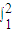 (2x2-
(2x2-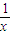 )dx;
)dx;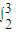 (
(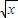 +
+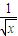 )2dx;
)2dx;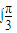 (sinx-sin2x)dx.
(sinx-sin2x)dx.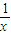 的原函数,将积分的上限、下限代入求值.
的原函数,将积分的上限、下限代入求值.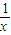 +2的原函数,将积分的上限、下限代入求值.
+2的原函数,将积分的上限、下限代入求值.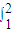 (2x2-
(2x2-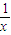 )dx=(
)dx=( x3-lnx)
x3-lnx)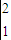
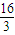 -ln2-
-ln2- =
= -ln2.
-ln2.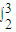 (
(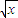 +
+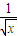 )2dx=
)2dx=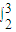 (x+
(x+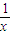 +2)dx
+2)dx x2+lnx+2x)
x2+lnx+2x)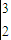
 +ln3+6)-(2+ln2+4)
+ln3+6)-(2+ln2+4) +
+ .
.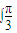 (sinx-sin2x)dx=(-cosx+
(sinx-sin2x)dx=(-cosx+ cos2x)
cos2x)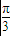
 -
- )-(-1+
)-(-1+ )=-
)=- .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com