
(满分12分)
设某物体一天中的温度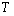 是时间
是时间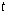 的函数,已知
的函数,已知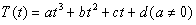 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的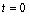 ,中午12:00以后相应的
,中午12:00以后相应的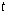 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的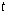 取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(I)求该物体的温度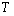 关于时间
关于时间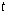 的函数关系式;
的函数关系式;
(II)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
科目:高中数学 来源: 题型:
(本小题满分12分)
设进入某商场的每一位顾客购买甲种商品的概率为![]() ,购买乙种商品的概率为
,购买乙种商品的概率为![]() ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记![]() 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求![]() 的分布列及期望。
的分布列及期望。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市鱼台一中高二上学期期中考试理数试卷(带解析) 题型:解答题
(本题满分12分)设平面直角坐标系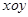 中,设二次函数
中,设二次函数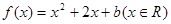 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(1)求实数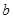 的取值范围;
的取值范围;
(2)求圆C 的方程;
(3)问圆C 是否经过某定点(其坐标与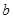 无关)?请证明你的结论.
无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014届甘肃省高二第二次月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)设某物体一天中的温度 是时间
是时间 的函数:
的函数: ,其中温度的单位是
,其中温度的单位是 ,时间单位是小时,
,时间单位是小时, 表示12:00,
表示12:00, 取正值表示12:00以后.若测得该物体在8:00的温度是
取正值表示12:00以后.若测得该物体在8:00的温度是 ,12:00的温度为
,12:00的温度为 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.
(1)写出该物体的温度 关于时间
关于时间 的函数关系式;
的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;
(3)如果规定一个函数 在区间
在区间 上的平均值为
上的平均值为 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三第一次质量检测理科数学卷 题型:解答题
(满分12分)
设某物体一天中的温度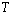 是时间
是时间 的函数,已知
的函数,已知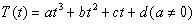 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的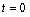 ,中午12:00以后相应的
,中午12:00以后相应的 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的 取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(I)求该物体的温度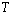 关于时间
关于时间 的函数关系式;
的函数关系式;
(II)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com