
 ,则
,则 的取值范围是 .
的取值范围是 .  所在的直线为x轴,以
所在的直线为x轴,以 所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据动点的位置得到自变量的取值范围,做出函数的范围,即要求得数量积的范围.
所在的直线为x轴,建立坐标系,写出要用的点的坐标,根据两个点的位置得到坐标之间的关系,表示出两个向量的数量积,根据动点的位置得到自变量的取值范围,做出函数的范围,即要求得数量积的范围. 解:以
解:以 所在的直线为x轴,以
所在的直线为x轴,以 所在的直线为x轴,建立坐标系如图,
所在的直线为x轴,建立坐标系如图, ,
,
 ,
, =(2,
=(2, ),
), =
= ,
, ,
, ≤4
≤4

科目:高中数学 来源: 题型:
|
| ||
|
|
|
| ||
|
|
| AM |
| AN |
查看答案和解析>>
科目:高中数学 来源: 题型:
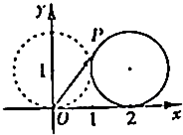 (1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,| OP |
|
| ||
|
|
|
| ||
|
|
| AM |
| AN |
查看答案和解析>>
科目:高中数学 来源:2012年普通高等学校招生全国统一考试上海卷数学文科 题型:022
在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足 ,则
,则![]() ·
·![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高一上学期期末考试数学试卷(解析版) 题型:解答题
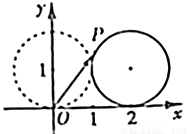
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0, 1),此时圆上一点P的位置在(0, 0),圆在x轴上沿正向滚动。当圆滚动到圆心位于(2, 1)时, 的坐标为______.
的坐标为______.
(2)(5分)在矩形ABCD中,边AB、AD的长分别为2、1,若M、N分别是边BC、CD上的点,且满足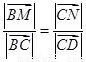 ,则
,则 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com